PRODUCTION AND PROPAGATION OF WAVES
Properties of Waves
Subject: Physics
Theme: PRODUCTION AND PROPAGATION OF WAVES
Topic: Production of mechanical waves
Sub Topic: Properties of Waves
Date: dd/mm/yyyy
Class: S.S.S 2
Duration: 40 Minutes
No of Learners: 40
Learning Objectives: By the end of the lesson learners should be able to:
1. List and explain the properties of waves
The properties of waves include; Reflection, Refraction, Interference, Diffraction, and Polarization.All waves exhibit the following properties:
➢ Reflection
➢ Refraction
➢ Diffraction
➢ Interference
Apart from the properties listed above only transverse waves has another properties called
➢ Polarization.
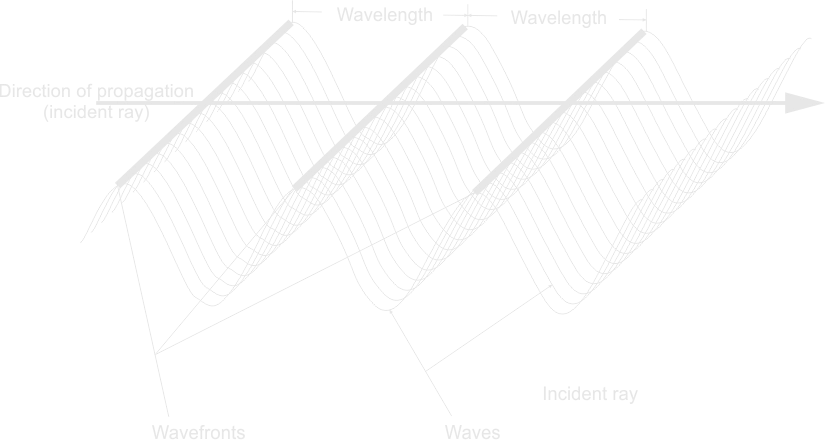
1. Reflection of waves:
Waves are reflected upon encountering a barrier. If the barrier is plane, the angle of incidence is equal to the angle of reflection. The frequency, speed and wavelength of the waves remain unchanged as long as they remain in the same medium after reflection.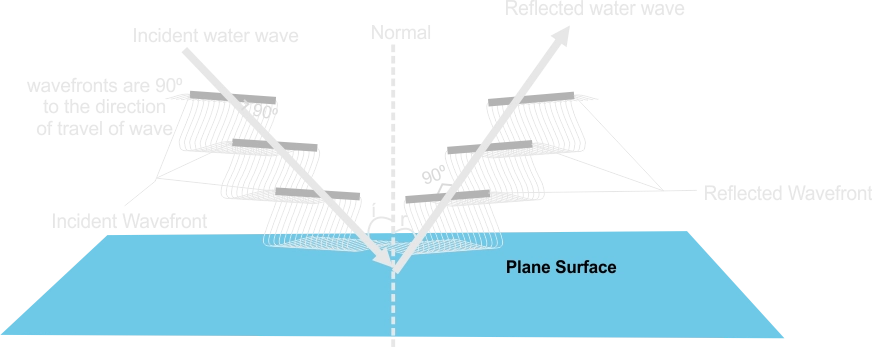
Laws of Reflection: When a wave strikes an interface, the angle of incidence measured to the normal of the interface is equal to the angle of reflection.
LAWS OF REFLECTION
1. The incident ray, the reflected ray and the normal, at point of incidence, all lie on the same plane.2. The angle of incidences is equal to the angle of reflection.
2. Refraction of wave:
Refraction is the change in the speed and direction of the waves as they cross the boundary between two media of different densities.The wave travels more slowly in shallow water compared to deep water.
The angle of incidence (i) is the angle the direction of the incident wavefront makes with the normal at the boundary surface. The angle of refraction (r) is the angle the direction of the refracted ray makes with the normal to the plane boundary.
N/B.
1. It is important to note that during refraction, the wavelength remains constant.
2. Refractive index is the ratio of the sine of the incident angle (i) to the sine of the angle of refraction (r). It is also the ratio of the velocity of the wave in the first medium (v1) to the velocity in the second medium (v2).
The wavelength decreases and the direction shift as the wave hit the more shallow side.
3. The amount by which a wave is refracted by a material is given by the refractive index of the material. The directions of incidence and refraction are related to the refractive indices of the two materials by Snell's law.
Waves travel slower in shallower water.
LAWS OF REFRACTION
1. The incident ray, refracted ray and the normal at the point of incidence; all lie on the same plane.2. The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant for a given pair of media.
The second law is known as Snell’s law.
n = sin i/sin r
1n2 = sin i/sin r
The refractive index, 1n2 of medium 1 with respect to medium 2 is related to the speeds of the wave in the two media as follows.
Refractive Index, 1n2 = Velocity of wave in 1 ÷ Velocity of wave in 2
Refractive Index, 1n2 = v1/v2
Since the frequency (f) of the wave remains constant during refraction.
v1 = fλ1
v2 = fλ2
where λ1, λ2 are the wavelength of the waves in medium 1 and 2 respectively
Hence, 1n2 = v1/v2
1n2 = fλ1/fλ2
1n2 = λ1/λ1
1n2 = Velocity of light in medium 1 ÷ Velocity of light in medium 2
1n2 = Velocity in deep water ÷ Velocity in shallow water
NOTE: n = sin i/sin r
The constant, n, is known as the refractive index of the second medium with respect to the first medium. It is a number which gives a measure of refraction or bending of light as it travels from one medium to another.
As the ray of light travels from air to glass, the refractive index can be written as: ang = sin i/sin r
Principle of reversibility states that the path of light ray is reversible.
Hence, From the principle of reversibility of ligh,
ang = 1/gna
Furthermore,
ang = speed of light in air (medium 1, incidence medium)/speed of light in glass (medium 2, refractive medium)
Refraction of ray
3. Diffraction of wave:
This is the spreading out of a wave on passing through a narrow opening.Diffraction occurs when the wavelength of the wave is longer than the width of the opening or the size of the obstacles. i.e The amount of diffraction depends on the wavelength of the wave compared with the size of the gap. That is, Diffraction effects are more pronounced when the size of the obstacle or opening is comparable to the wavelength of the wave.
Diffraction of wave
If the gap is smaller than the wavelength, the waves are mostly just reflected back.
If the barriers are placed closer to leave a narrow gap waves forms spherical wave fronts on passing through a narrow shit.
4. Interference of wave:
This is a phenomenon which occurs when two similar waves traveling in the same direction cross each other, they interact with each other. The interaction of waves with other waves is called wave interference.Interference of waves
Wave interference may occur when two waves that are traveling in opposite directions meet.Interference is the effect produced when two waves of the same frequency, amplitude and wavelength traveling in the same direction in a medium are superposed - as they simultaneously pass through a given point. The two waves pass through each other, and this affects the amplitude. How amplitude is affected by wave interference depends on the type of interference. Interference can be constructive or destructive.
(a) Constructive Interference: If the waves are in phase or step so that they travel the same distance at equal time and the crest or trough of the two waves arrive simultaneously or one is a complete wavelength ahead of the other. The resulting wave will build up to twice the amplitude of the two waves; this is called constructive or additive interference.
Constructive interference occurs when the crests of one wave overlap the crests of the other wave. As the waves pass through each other, the crests combine to produce a wave with greater amplitude.
Constructive Interference of waves
(b) Destructive Interference: Destructive interference occurs when the crests of one wave overlap the trough of another wave. As the waves pass through each other, the crests and troughs cancel each other out to produce a wave with zero amplitude.
Destructive Interference of waves
The task of determining the shape of the resultant demands that the principle of superposition is applied. The principle of superposition is sometimes stated as follows:
When two waves interfere, the resulting displacement of the medium at any location is the algebraic sum of the displacements of the individual waves at that same location.
| Displacement of Pulse A | Displacement of Pulse B | Resulting Displacement | Displacement of Pulse A and B = Resulting Displacement |
|---|---|---|---|
| +1 | +1 | +2 | |
| -1 | -1 | -2 | |
| +1 | -1 | 0 | |
| +1 | -2 | -1 |
|
| +2 | -1 | +1 |
|
5. Polarization of wave:
This is an exclusive property of transverse waves only. It is the production of transverse vibration in only one plane. A transverse wave which vibrates in only one plane is said to be plane-polarized.A light wave that is vibrating in more than one plane is referred to as unpolarized light. Light emitted by the sun, by a lamp in the classroom, or by a candle flame is unpolarized light. Such light waves are created by electric charges that vibrate in a variety of directions, thus creating an electromagnetic wave that vibrates in a variety of directions.
In general, it is helpful to picture unpolarized light as a wave that has an average of half its vibrations in a horizontal plane and half of its vibrations in a vertical plane. Plane polarization of light means the fluctuations or vibrations are constructed to vibrate only in one plane perpendicular to the direction of the light.
It is possible to transform unpolarized light into polarized light. Polarized light waves are light waves in which the vibrations occur in a single plane. The process of transforming unpolarized light into polarized light is known as polarization.
Polarized light can be produced by passing an ordinary light through a polarizer called Polaroid or crystal of calcite, tourmaline or quartz. The arrangement of molecules within this polarizer will only permit the passage of light in a particular plane and then absorb light due to other vibration. Thus, when an unpolarized light is passed through a polarizer, the emergent light consists in only one plane.
2. List and explain Types of Polarization:
(i) Linear Polarization: In linear polarization, the electric field of light is limited to a single plane along the direction of propagation, the electric field vibrates in a certain linear direction perpendicular to the wave axis, and the magnetic field vibrates in a direction that is perpendicular to both, the advancement axis and direction of the electric field. The direction of polarization is considered to be the direction of the electric field vibration. The polarization can take place in any other direction perpendicular to the wave axis. Rotation of the polarization by 180° does not lead to a rationally different state.Linear Polarization
The propagation of the occurring electric field will be in a circular motion.
Circular polarization and linear polarization can be considered as special cases of elliptical polarization.
3. List and explain methods Used in the Polarization of Light:
(i) Polaroid(ii) Polarization by Transmission
(iii) Polarization by Reflection (from smooth surface)
(iv) Polarization by Scattering (by small particles)
(v) Polarization by Refraction
(vi) Polarization by Double Refraction (through crystals)
(vii) Polarization by Selective Absorption (in certain crystals)
(i) Polarization by Scattering: When light travels through a medium, atoms of the medium (also the dust present in the medium) vibrate and produce electromagnetic waves. These waves are radiated outwards and thus the light is scattered. In this entire process, absorption and remission of light waves occur throughout the material. The scattered light is also known as partially polarized. Transmission of these partially polarised lights causes glare.
(ii) Polarization by Reflection: When unpolarized light is made to fall on a non-metallic surface, at a particular angle, the surface reflects the polarized light. In this process, the angle of incidence and the non-metallic surface plays an important role to regulate the magnitude of polarization.
(iii) Polarization by Refraction: Refraction is when a light wave travels from one medium to another, it changes its direction and speed. This refracted beam attains some degree of polarization. In the majority of the cases, polarization by refraction occurs in the plane which is perpendicular to the surface.
(iv) Polarization by Transmission: In this method, involves the use of filter materials that have special chemical composition. They are known as Polaroid filters. These polaroid filters can block one of the two planes of electromagnetic waves. When the unpolarized light is transmitted through these polaroid filters, it filters out one-half of the vibrations of the light in a single plane. This polarized light has one half of the intensity.
4. List Applications of Polarization of Light:
(a) Polarization is used in the production of glare-reducing sunglasses to reduce the intensity of incident light and to eliminate reflected light glare.(b) In many industries, polaroid filters are used for stress analysis tests on transparent plastics.
(c) Three-dimensional movies are produced and shown with the help of polarization.
(d) Polarization is used for differentiating between transverse and longitudinal waves.
(e) To cut the refractions, Fishermen, Skiers, motorists, sportsmen need special sunglasses. In the production of these special sunglasses polarization of light is used.
(f) Many photographers use polarizers to capture the perfect scene.
(g) Polarization microscopes are used in geological studies to identify minerals.
(h) Infrared spectroscopy uses polarization.
(i) In Chemistry, the chirality of organic compounds is tested using polarization techniques.
(j) It is used in seismology to study earthquakes.
(k) To study the physics of the early universe, the effect of polarization is used.
(l) Polarization is used to know the source of radiation and scattering.
(m) To characterize the stress-strain distribution in the prototypes, polarization is used.
(n) Polarization is used to identify thermally tempered lenses.
(o) In ophthalmic instruments, to eliminate strong reflection from a patient's cornea, the phenomenon polarization of light is used.
(p) As light passes through the atmosphere polarization of light is observed.
(q) Through polarization the scattered light is known to give rise to various colours in the sky.
5. Solve practical problem on waves:
Example 1.The wavelength and velocity of a set of plane waves travelling in a medium are 60 cm and 320 cm/s respectively. It meets a plane refracting surface at an angle of incidence of 600. Its velocity after refraction is 280 cm/s. Calculate the wavelength of the waves in the second medium and also the angle of refraction.
Solution
λ1 = 60 cm
v1 = 320 cm/s
i = 600
v2 = 280 cm/s
refractive index 1n2 = sin i / sin r = v1 / v2 = λ1 / λ2
1n2 = sin 600 / sin r = 320 / 280 = 60 / λ2
320 / 280 = 60 / λ2
λ2 = 280 x 60 / 320
λ2 = 52.5 cm
sin 600 / sin r = 320 / 280
sin 600 / sin r = 1.143
sin r = sin 600 / 1.143
sin r = 0.7577
r = 49.260
Example 2.
1. The speed of light in air is 3 x 108 m/s. If the refractive index of water is 4/3, what is the speed of light in water?
SOLUTION
Refractive index of water = speed of light in air ÷ speed of light in water
Speed of light in water = speed of light in air ÷ refractive index of water
Speed of light in water = (3 x 108) ÷ 4/3
Speed of light in water = 2,25 x 108 m/s
Example 3.
The speed light in a glass medium is 1.80 x 108 m/s. If the speed of light in air is 3 x 108 m/s, what is the refractive indcN of the glass?
SOLUTION
Refractive index of glass = speed of light in air / speed light in glass
Refractive index of glass = (3 x 108) / 1.80 x 108
Refractive index of glass = 1.667
Example 4.
Light of wavelength 5 x 107m has a speed of 3 x 108 m/s in air. What is its wavelength in glass of refractive index 1.5?
SOLUTION
Refractive index of glass = speed of light in air / speed light in glass
Refractive index of glass = wavelength in air / wavelength in glass
wavelength in glass = wavelength in air / Refractive index of glass
wavelength in glass = 5000 x 10-8 / 1.5
wavelength in glass = 3333 x 10-8m
A ray of light travelling in air is incident at an angle of 30° on the surface of water of refractive index 4/3. What is the angle of refraction?
SOLUTION
n = sin i / sin r
sin r = sin i / n
sin r = sin 300 ÷ 4/3
sin r = 0.375
r = sin-1 0.375
r = 220
Example 6.
The speeds of light in air and in glass are 3.0 x 108 m/s and 1.8 x 108 m/s respectively. If the angle of refraction of a ray of light incident on an air/glass interface is 300. What is the sine of the angle of incidence?
SOLUTION
n = speeds of light in air / speed of light in glass
n = (3.0 x 108) / (1.8 x 108)
n = 1.667
But n = sin i / sin r
sin i = n x sin r
sin i = 1.667 x sin 300
sin i = 1.667 x 0.5
sin i = 0.83
Example 7.
A ray of light which is incident normally on an air-glass interface is, upon refraction in the glass, deviated through an angle of?
A. 0° B. 45° C. 60° D. 90°
SOLUTION
n = sin i / sin r
sin r = 1/n x sin i
sin r = 1/n x sin 900
sin r = 1/n x 0
sin r = 0
r = sin-1 0
r = 0
The angle of deviation is zero.
A. 0°
Example 8.
A ray of light AC travelling in air is refracted along the path CD in glass as shown in the figure 8.1. If points A and D lie on a circle centred on C, the refractive index of the glass is given by what ratio?
SOLUTION
n = sin i / sin r
n = sin ACD / sin DCE
n = (AB/AC) / (DE/CD)
n = AB/DE
n = CG/CF
[Note that AC = CD, AB = CG and DE = CF]
Example 9.
The refractive index of a medium is √2. What is the critical angle?
SOLUTION
sin c = 1/n
sin c = 1/√2
c = sin-1 x 1/√2
c = 450
Example 10.
The critical angle for light travelling from a transparent medium to air is measured as 34°. What is the refractive index of the medium?
SOLUTION
n = 1/sin c
n = 1/ sin 340
n = 1.79
Two rays of light which are equally inclined to the vertical emanate from a point below the surface of a pool of water (refractive index = 4/3). If the two rays are inclined to each other at an angle of 80° in the water, what is the angle between the rays when they emerge into air?
SOLUTION
From the figure above
sin r/sin 400 = 4/3
sin r = 4/3 x sin 400
sin r = 0.857
r = sin-1 0.857
r = 590
Example 12.
A ray of light is incident on an air/glass interface (see figure 12.1). If the reflected glass ray is perpendicular to the refracted ray aS glass has a refractive index of 1.50, what is the approximate angle of incidence?
SOLUTION
The angle of refraction, r = 1800 - (900 + i)
r = 900 - i
n = sin i / sin r
n = sin i / [sin (900 - i)]
n = sin i / cos i
n = tan i
1.50 = tan i
i = tan-1 1.50
i = 56.30
Example 13
A ray of light is incident on one side of a parallel-sided glass block of refractive index 1.50 and emerges from the other side after refraction through the block. If the angle of incidence is 40°, what is the angular deviation of the emergent ray?
SOLUTION
The emergent ray is parallel to the incident ray, hence the angular deviation is zero.
The refractive index for a given transparent medium is 1.4. What is the minimum angle required for total internal reflection to take place in the medium?
SOLUTION
n = 1/sin c
sin c = 1/n
sin c = 1/1.4
sin c = 0.714
c = sin-1 0.714
c = 460
Example 15.
An incident ray DB is inclined at an angle of 600 to the interface AB. If the refracted ray BC lies along the surface, what is the refractive index of the medium?
SOLUTION
Critical angle, c = 900 - 600
c = 300
n = sin 900 / sin c
n = 1/0.5
n = 2
Example 16.
In figure 16.1, a ray of light CD moves from a glass block into air. If AC = 5cm and BC = 2 cm, what is the refractive index of the glass?
SOLUTION
critical angle, n = real depth / apparent depth
c = AC/AB
AB = AC - BC
AB = 5 - 2
AB = 3 cm
n = 5/3
n = 1.67
Example 17.
A ray of light travelling in glass of refractive index 1.5 is incident at an angle of 450 at the glass/air boundary. Which of the following figures correctly illustrates the path of the ray?
SOLUTION
The important point to investigate here is whether or not the critical angle is exceeded.
n = 1/sin c
sin c = 1/1.5
sin c = 0.667
c = sin-1 0.667
c = 41.80
Since the angle of incidence at the glass/air interface is greater tha thecritical angle, the ray is totally internally relected.
Hence the correct option is (B.)
Example 18. A air A ray of light is incident on a glass block as shown in figure 18.1. What is the refractive the index of the glass?
SOLUTION
Angle of incidence, i = 900 - 600
i = 300
Angle of reflection, r = 900 - 720
r = 180
n = sin i / sin r
n = sin 300 / sin 180 n = 1.62
Rationale:
Longitudinal waves are waves which travel in a direction parallel to the vibrations of the medium. E.g spring by alternatively compressing and expanding one end or by moving.
Transverse waves are waves which travel perpendicularly to the direction of the vibrations producing the waves. E.g light waves, radio waves and X-rays.
The properties of wave include: Reflection, Refraction, Diffraction, Interference and Polarization (only in light wave).
Prerequisite/ Previous knowledge:
Production and propagation of wave.Learning Materials:
A beaker containing water, a stick of broom and a leaf, Production of mechanical waves, pulsating systems and waveform.Reference Materials:
1. New School Physic for Senior Secondary Schools, by M. W. Anyakowa.2. Lamlas's SSCE and UTME, by O. Ajaja and H. B. Olaniyi.
3. Okeke P.N and etal (2011), Macminian, Senior Secondary School Physics, New Edition.
4. Farinde E.O and etal (2015), Essential Physics. 6th Edition,
Lesson Development:
| STAGE | TEACHER'S ACTIVITY | LEARNER'S ACTIVITY | LEARNING POINTS |
|---|---|---|---|
| STEP I: PREVIOUS KNOWLEDGE full class session |
The teacher asks learners questions based on previous knowledge. 1. What does ‘the light from the sun is unpolarised’ means and how does it get polarized? 2. Mention different types of polarization? 3. What is the polarization of Light? 4. What causes the polarization of Light? 5. What are Flexible Waves? 6. Why is the polarization of Light critical? 7. Can the light of different polarization interfere? 8. What is the wave equation? |
Learners' response to teacher's question. 1. ‘the light from the sun is unpolarised’: It means that the light emitted by the sun travels in all the given directions i.e in different planes. And while being transmitted through a distance it gets semi polarized and only gets polarized when its angle of reflection is equal to the angle of polarization. Because the light of the sun takes all directions, it is said to be unpolarized light. When unpolarized light falls on the transparent surface at an angle of incidence equal to the polarization angle also called Brewster's angle, it is called plane-polarized. When the unpolarized light is passed through a polarizing sheet, it becomes polarized. 2. Different types of polarization are: Linear Polarization, Circular Polarization and Elliptical Polarization. The different types of polarization may also be study under: (a) Electronic polarization: The displacement occurring in dielectric elements and minerals between a positive charge and negative charge results in Electronic polarization. (b) Linear polarization: It means that light is confined to one plane only. (c) Space charge polarization: It means the accumulation of the charge at electrodes and their interface. (d) Ionic polarization: It occurs in dielectric metals which have atomic bonds between them. 3. Polarization of Light: An event caused by the vibration of light waves limited to a specific plane is known as polarisation. With normal light from the feed, vibration usually occurs in the distribution path across all active aircraft. 4. Causes the polarization of Light: Polarization additionally takes place when light is scattered even as touring via a medium. while light moves the atoms of a material, it'll regularly set the electrons of these atoms into vibration. The vibrating electrons then produce their electromagnetic wave that is radiated outward in all instructions. 5. Flexible Waves: Waves where particle movements depend on the direction of wave motion. For example, when you throw a stone, it creates waves in the water and sounds like air. 6. Why polarization of Light critical? Polarization is a crucial property of light that affects even the optical systems that don't explicitly measure it. The polarization of light influences the point of interest of laser beams affects the reduced-off wavelengths of filters and can be critical to saving you unwanted returned reflections. 7. Can the light of different polarization interfere? In impact, polarized mild waves having their vibration instructions oriented parallel to every different can integrate to provide interference, while those which can be perpendicular do not intervene. 8. y = A sin 2𝜋/𝜆(𝑣𝑡 − 𝑥) y = Vertical displacement x = Horizontal displacement A = Amplitude ω = angular velocity (rads⁻¹) ϕ = phase angel, measured in radian (rad) ω = 2πf |
Confirming previous knowledge. |
|
|
|||
| STEP II: INTRODUCTION full class session |
The teacher review with learners PRODUCTION & PROPAGATION OF MECHANICAL WAVES & ELECTROMAGNETIC WAVES Production of Mechanical waves require materials medium for their propagation (Transverse and longitudinal waves). Examples are water wave, wave generated in a spring or rope, sound wave while Production of Electromagnetic wave does not require material medium for its propagation (only longitudinal waves). Examples are light ray, radio wave etc. wave propagation is a term used to describe the way waves travel or move. Vibration of particles in air produce sound waves, and vibration of charged particles generates electromagnetic waves. Longitudinal Wave: For longitudinal waves, the displacement of the particles is parallel to the wave propagation direction. Particles do not move in the tube with the waves. They simply rock back and forth around individual equilibrium positions. Choose a single particle and watch it move. The waves appear to move from left to right in the compressed area (that is, the pressure wave). The P wave (primary wave) of an earthquake is an example of a longitudinal wave. The P wave moves fastest and arrives first. Transverse Wave: In transverse waves, the displacement of the particles is perpendicular to the wave propagation direction. Particles do not move with the waves. They only sway up and down around their equilibrium positions as the waves pass. Choose a single particle and watch it move. The S wave (secondary wave) of an earthquake is an example of a transverse wave. The S wave travels slower than the P wave and arrives in a few seconds. How does Transverse Waves exhibit Polarization? A transverse wave is a wave that sways (vibrates) up and down perpendicular to the wave propagation direction. Due to the three dimensions, there are two directions perpendicular to the propagation direction. Therefore, if the wave is propagating in the Z direction (that is, if the Z-axis is selected as the direction of travel of the wave), the wave can oscillate in the X or Y direction, or a combination of these overlay directions. Therefore, the shear wave has two polarizations, one for each direction of propagation. If you have a polarized light-sensitive medium (such as a polarizing element for eyeglasses), you can detect the polarized light. For example, consider two polarisations. Align one to the X-axis, then rotate the other. You can see that the light intensity is cos2θ. Where θ is the relative angle between the preferential directions of the modulator. |
Learners listen to teacher and contributed Waves are fundamental phenomena in nature that carry energy and information from one place to another. They can be broadly categorized into two main types: longitudinal waves and transverse waves, each with unique properties and characteristics. Longitudinal Waves: Direction of Particle Displacement: In a longitudinal wave, the particles of the medium (the material through which the wave travels) move in a direction parallel to the direction of the wave itself. This means that they oscillate back and forth along the same line as the wave. Compression and Rarefaction: In a longitudinal wave, regions where particles are pushed closer together are called "compressions," while regions where particles are spread apart are called "rarefactions." These regions alternate as the wave passes through the medium. Examples: Sound waves are a common example of longitudinal waves. When you hear a sound, it's because of the compressions and rarefactions of air particles that travel to your ears. Transverse Waves: Direction of Particle Displacement: In a transverse wave, the particles of the medium move perpendicular (at right angles) to the direction of the wave. They move up and down or side to side in a vibrational motion. Crests and Troughs: Transverse waves have high points called "crests" and low points called "troughs." These crests and troughs form a repeating pattern as the wave passes through the medium. Examples: Light waves and electromagnetic waves, such as radio waves and microwaves, are transverse waves. You can think of light waves as oscillations of electric and magnetic fields perpendicular to the wave's direction. Common Characteristics of Both Wave Types: (i) Wavelength: Wavelength is the distance between two consecutive points in a wave that are in phase with each other. For longitudinal waves, this is the distance between two consecutive compressions or rarefactions. For transverse waves, it's the distance between two crests or two troughs. (ii) Frequency: Frequency is the number of complete cycles (or oscillations) a wave undergoes per unit of time. It's measured in Hertz (Hz). (iii) Amplitude: The amplitude of a wave is the maximum displacement of particles from their resting position. In a transverse wave, it's the distance from the crest (or trough) to the resting position. In a longitudinal wave, it's the maximum compression or rarefaction from the equilibrium. |
Developing the idea of properties of wave motion. |
| STEP III: EXPLORATION Properties of Waves |
The teacher guides learners to relate the explanation above to list and explain properties of waves. | Learners' expected response, during propagation the waves may undergo Reflection; Refraction; Diffraction; Interference and Polarization 1. Reflection of waves: This is the change in the direction of waves when they hit an obstacle. E.g straight and parallel waves are set up from a plan metal strip standing upright in the water. 2. Refraction of waves: This occurs between two media, when wave direction of propagation changes as it enters a different medium. When straight waves pass from deep to shallow water, their wavelength becomes shorter. Duration this process, the frequency remains the same, but the wavelength varies. 3. Diffraction: This is the phenomenon where by waves bend round obstacles. It is also the speeding of waves after passing through tiny opening a hole or slit. 4. Interference: This occur when two waves from a source cross each other path i.e the interaction of two (coherent) waves which moves simultaneously through the same medium. It is referred to as constructive interference. 5. Polarization: It simply means that confinement of waves in one direction occurs only in transverse waves. |
Properties of waves |
| STEP IV: DISCUSSION APPLICATION OF PLANE-POLARIZED LIGHT |
The teacher guides the students as follow: What is Plane-polarization and List the application of plane-polarized wave. |
Learners expected respond. Plane polarization of light means the fluctuations or vibrations are constructed to vibrate only in one plane perpendicular to the direction of the light. Application of plane-polarized wave are: 1. Production of three dimension films. 2. Determination of concentration of sugar solution. 3. Polarized cameras. 4. Sun glasses to reduce the intensity of light. |
Plane-polarized wave and its application of plane-polarized wave. |
|
|
|||
| STEP V: APPLICATION Practical problem on waves |
The teacher guides students on how to solve practical problem on waves. Example 1. The speed light in a glass medium is 1.80 x 108 m/s. If the speed of light in air is 3 x 108 m/s, what is the refractive indcN of the glass? SOLUTION Refractive index of glass = speed of light in air / speed light in glass Refractive index of glass = (3 x 108) / 1.80 x 108 Refractive index of glass = 1.667 Example 2. A ray of light which is incident normally on an air-glass interface is, upon refraction in the glass, deviated through an angle of? A. 0° B. 45° C. 60° D. 90° SOLUTION n = sin i / sin r sin r = 1/n x sin i sin r = 1/n x sin 900 sin r = 1/n x 0 sin r = 0 r = sin-1 0 r = 0 The angle of deviation is zero. A. 0° Example 3. The refractive index of a medium is √2. What is the critical angle? SOLUTION sin c = 1/n sin c = 1/√2 c = sin-1 x 1/√2 c = 450 |
The students listen attentively | Practical problem on waves |
| STEP VI: EVALUATION | The teacher asks the learners questions. 1. What are the conditions necessary for production of stationary wave? 2. What are the conditions necessary for formation of interference wave pattern? 3. What are the conditions necessary for total internal reflection? 4. A ray of light travelling in air is incident at an angle of 30° on the surface of water of refractive index 4/3. What is the angle of refraction? |
The learners answer the teacher's questions. 1. Conditions necessary for production of stationary wave - Two waves must be traveling in opposite directions. - Incident and reflected waves must have the same frequency/wavelength. - Incident and reflected waves must have equal amplitude. - There must be superimposition. - There must be a barrier 2. Conditions necessary for formation of interference wave pattern - Two sources must be involved. - The two sources must be coherent/have a constant phase difference as well as the same frequency and amplitude. - The waves that are interfering must have the same amplitude - The distance between the sources must be of the order of the wavelengths of the waves. 3. Conditions necessary for total internal reflection - The wave must be traveling from a denser medium to a less dense medium - The angle of incidence of the wave in the denser medium must be greater than the critical angle for the medium. 4. SOLUTION n = sin i / sin r sin r = sin i / n sin r = sin 300 ÷ 4/3 sin r = 0.375 r = sin-1 0.375 r = 220 |
Ask the learners questions to assess the achievement of the set objectives. |
| CONCLUSION | The teacher concluded the lesson. Propagation: Both Mechanical and Electromagnetic waves propagate energy and information through the medium without permanently displacing the particles. The medium oscillates in response to the passage of the wave, and energy is transmitted through the wave's motion. Understanding the differences between longitudinal and transverse waves is essential in various scientific fields, from physics and engineering to telecommunications and music. It's crucial for comprehending the nature of waves and their practical applications in our daily lives. |
Learners listen to the teacher. | Application of wave. |
|
|
|||
| ASSIGNMENT | The teacher gives learners a take home. | 1. A vibrating plate is used to generate waves in a pool of water. The distance between successive troughs is 7cm and a crest travels from the vibrator to the edge of the pool, 52.5cm away, in 2.5 sec. Calculate the frequency of the vibrator. 2. A rarefaction and an adjacent compression of a sound wave travelling in the air are separated by a distance of 15cm. If the velocity of sound in air is 330 m/s. What is the frequency? 3. If the speed of sound in air is 340 m/s, what is the period of vibration of sound waves of wavelength 1.7m? 4. Which of the following phenomena does not apply to longitudinal waves? ➢ interference ➢ refraction ➢ diffraction ➢ polarization 5. Which of the following waves is both mechanical and transverse? ➢ radio ➢ sound ➢ water ➢ x-rays 6. y = A sin 2𝜋/𝜆(𝑣𝑡 − 𝑥) represents a wave train in which y is the vertical displacement of a particle at a distance x from the origin in the medium through which the wave travelling. What does each variables in the equation represents. |
Improving their level of understanding of waves. |