PRODUCTION AND PROPAGATION OF WAVES
Production of mechanical waves
Subject: Physics
Theme: PRODUCTION AND PROPAGATION OF WAVES
Topic: Production of mechanical waves
Sub Topic: Wave Motion
Date: dd/mm/yyyy
Class: S.S.S 2
Duration: 40 Minutes
No of Learners: 40
Learning Objectives: By the end of the lesson learners should be able to:
1. Identify and Define a wave and wave motion
Wave: is a disturbance that transfers energy from one point to another without transferring matter.
Wave motion: is process of transferring a disturbance from one point to another without any transfer of particles of the medium.
2. List and explain types of waves
Waves are broadly classified into two types:a. Based on the medium of propagation: mechanical wave and electromagnetic wave.
b. Based on the wave direction with the direction of vibration of the particle: Progressive or Travelling wave and Standing or stationary wave.
(A) Types of waves: Based on the medium of propagation
1. Mechanical waves: A mechanical wave is the wave that requires material medium for its mode of propagation (or for it to transfer energy away from the source).Examples are waves travelling through springs, water waves, and sound waves.
2. Electromagnetic waves: Electromagnetic waves are waves that do not need material medium for its mode of propagation (or for it to transfer energy away from the source).
Examples are radio waves, (GXUVIMR) gamma rays, x-rays, ultra-violet rays, visible light, infrared-ray, micro waves and radio waves. Electromagnetic waves travels at the speed of light (3.0Γ108m).
Electromagnetic Spectrum (increasing wavelength):
1. Gamma rays
2. X-rays
3. Ultraviolet rays
4. Visible light (ROYGBIV)
5. Infrared rays
6. Microwaves
7. Radio waves
(B) Types of waves: Based on the direction of vibration of the particle
1.Progressive or Travelling wave: is a wave which travels along a medium transferring energy from one part of the medium to another. The progressive wave can be divided into transverse and longitudinal wavesi. Transverse waves: A transverse wave is a wave in which travel perpendicularly to the direction of the vibrations producing the waves eg: Water waves, light waves, waves on a string/rope, all electromagnetic waves, etc.
ii. Longitudinal wave: Longitudinal waves are waves which travel in a direction parallel to the vibrations of the medium eg: Sound waves, compression waves in a slinky, ultrasonic waves, pressure waves in fluids and seismic P-waves, etc.
2. Standing or stationary wave: this is formed when two waves travelling in the opposite direction meets or by superimposition of incident wave and its reflection. The amplitude of the standing wave varies along the wave. Examples of standing waves are; waves generated by piano, guitar string, two people shaking a jump rope, etc.
3. List and explain TERMS USED IN DESCRIBING WAVES
1. The amplitude (A): is the maximum displacement of a particle from its rest or mean position. It is measured in meter (m).
2. The period (T): is the time required for a particle to perform one complete cycle or oscillation
π = 1/π -----(1)
π = 1/π
3. Frequency (f): is the number of complete cycles made in one seconds. It is measured in Hertz (Hz).
4. Wavelength (Ξ»): is the distance between two successive crests or troughs. Wavelength could also be defined as the distance covered by wave after one complete oscillation. For transverse waves, it is the distance between two successive crests or troughs while for longitudinal wave, it is the distance between successive compressions or rarefactions. It is measured in meter (m).
5. Wave-velocity (v): is the distance traveled by the waves in one second. The S.I unit is m/s.
6. Phase: is made of particles that are at the same vertical distance from their point of rest and are also moving in the same direction. Particles which are at the same vertical direction from their positions of rest and are moving in the same direction are said to be in phase.
7. Cycle: is a complete oscillation or vibration of a wave particle.
4. Explain MATHEMATICAL RELATIONSHIP of terms use in wave
π£ = π€ππ£π-π£ππππππ‘π¦ (m/s)π = πππππ’ππππ¦ (π»π§)
π = π€ππ£ππππππ‘h (π)
π = ππππππ (π )
πππππππ‘π¦ = πππππ’ππππ¦ Γ π€ππ£ππππππ‘h
π£ = ππ
π£ = πππ π‘ππππ π‘πππ£πππππ ππ¦ π€ππ£π Γ· ππππππ πππππππ π‘πππ π‘ππππ
π£ = π/π
From equation 1, π = 1π
We have:
π£ = π/π
π£ = ππ
1π = 3600 = 2π
π£ = 2ππ
Recall, Angular speed π = 2ππ
A wavelength is measured from crest to crest, or tough to tough, half wavelength is shown in the first row image while full wavelength is shown in the second row in the image. Twice the distance between nodes is the same as the distance from one peak to the next, so the wavelength would be twice the distance between the two nodes.
If the distance from point 0 to point 1 is meter, then the wavelength of the first standing wave would be 2 meters.
Example 1.
A string is stretched rightly between two points, 50cm apart. It is plucked at its centre and the velocity of the wave produced is 300 m/s. Calculate the number of vibrations made by the sting in one second.
Solution
L = 50cm = 0.50m
v = 300m/s
Ξ»/2 = L
Ξ»/2 = 0.50m
Ξ» = 2 x 0.50 = 1m
v = fΞ»
f = v/Ξ»
f = 300/1
f = 300Hz
Example 2.
A wave has a frequency of 4 Hz and a wavelength of 2 m. Find its speed.
Solution:
v = fΞ»
v = 4 Γ 2
v = 8 m/s
Example 3.
The period of a wave is 0.5 s. Find its frequency.
Solution:
f = 1/T
f = 1/0.5
f = 2 Hz
Example 4.
A wave travels 120 m in 6 seconds. Find its speed.
Solution:
v = distance/time
v = 120/6
v = 20 m/s
Example 5.
A wave travels at 330 m/s and has a wavelength of 0.75 m. Find its frequency.
Solution:
f = v/Ξ»
f = 330/0.75
f = 440 Hz
Example 6.
The speed of sound in air is 340 m/s. If a tuning fork produces sound waves with a frequency of 256 Hz, find the wavelength.
Solution:
Ξ» = v/f
Ξ» = 340/256
Ξ» = 1.33 m
Example 7.
A radio station broadcasts at a frequency of 100 MHz. Calculate the wavelength of the radio wave. [velocity of light = 3 x 108]
Solution:
Ξ» = v/f
Ξ» = 3 x 108 / 100 x 106
Ξ» = 3 m
Example 8.
A boat generates water waves with a wavelength of 5 m and a speed of 2 m/s. How long does it take for one complete wave to pass a fixed point?
Solution:
T = Ξ»/v
T = 5/2
T = 2.5 s
Example 9.
The distance between two successive crests in a ripple tank is 0.4 m. If 10 crests pass a point in 5 seconds, find the speed of the wave.
Solution:
frequency(f) is the number of complete cycles made in one seconds.
:. f = 10/5
f = 2 Hz
Ξ» = 0.4 m
v = fΞ»
v = 2 Γ 0.4 = 0.8 m/s
Example 10.
A radio station broadcasts at frequency of 300 KHz. If the speed of the wave is 3 x 108 ms-1, calculate the period and wavelength of the wave?
Solution π=1/π
π=1/1300 x 103
π = 3.3Γ10-6 π
π£ = π/π
π£ = 3Γ108 Γ· 3Γ105
π = 1000π or π = 1ππ
Example 11.
A long rope is fixed at its both ends and is made to oscillate at frequency of 4Hz. The successive crests are o.6 m apart.
(i) Calculate the speed of the wave.
(ii) At what frequency would the wavelength be 30 cm?
Solution.
π£ = ππ
π£ = 4Γ0.6
π£ = 2.4 π/π
When π = 30 ππ = 0.3 π
π = π£/π
π = 2.4/0.3
π = 8 π»π§
Example 12.
The frequency of vibrating source is 450 Hz and the velosity of the sound it produces in air is 330 m/s. Find how far the sound travels when the source completes 50 vibrations.
Solution
f = 450 Hz or 450 cycles per sec.
T = 1/f
T = 1/450
at 50 complete vibration,
T = 1/450 x 50
T = 1/9 secs.
v = 330 m/s
displacement (x or s) = velocity (v) x time (t)
s = vt
s = 330 x 1/9
s = 36.67 m
5. Derive and memorize the Mathematical representation of Progressive wave motion (Wave equation)
The dots on the graph represent the positions of the particles at that instant and the arrows indicate the direction of motion of these particles.
y = horizontal displacement of the particle from rest at a particular time
x = hππππ§πππ‘ππ πππππππππ‘π ππ π‘he π£πππππ‘πππ ππππ‘ππππ.
A = vibration of the particle A from its rest position from the right angle triangle
NOTE: 'A' from the Right Angle Triangle = 'A' the Amplitude of the wave, this was a term use in order for the students to prove and memorize the equation of the wave
ΞΈ = oscillation made at a given time
one complete oscillation = one wavelength
But one complete oscillation = the circumference of circle
circumference of circle = 2Ξ©r or 2Ξ©π₯, where x = r
:. 1π = 1 complete cycle = 3600 = 2Ξ©π₯
Hence, ΞΈ = 2Ξ©π₯/π
From the right Angle Triangle (Trigonometry),
sin ΞΈ = y/A
y = A sin ΞΈ
y = A sin (2Ξ©π₯/π) -------- (1) At t = 0 (at the origin)
Where:
π΄ = ππππππ‘π’ππ ππ π‘hπ π€ππ£π
π = π€ππ£ππππππ‘h ππ π‘hπ π€ππ£π
π¦ = π£πππ‘ππππ πππ πππππππππ‘ ππ π‘hπ π€ππ£π
π₯ = vππππ§πππ‘ππ πππππππππ‘π ππ π‘hπ π£πππππ‘πππ ππππ‘ππππ
The displacement after t seconds is given by:
y = A sin (ΞΈ - Ξ¦)
y = A sin [2Ξ©/π(π₯2 - π₯1)]
But displacement π₯ = velocity v x time t
π₯ = vt
Let π₯2 = π₯ and π₯1 = vt
or π₯2 = vt and π₯1 = π₯
:. y = A sin [2Ξ©/π (π₯ - vt)]
y = A sin (2Ξ©π₯/π - 2Ξ©vt/π)
But v = πf and π = 2ππ
:. y = A sin (2Ξ©π₯/π - 2Ξ©πft/π)
y = A sin (2Ξ©π₯/π - 2Ξ©ft) -------- (2)
y = A sin (2Ξ©π₯/π - πt) -------- (3)
or y = A sin (πt - 2Ξ©π₯/π) -------- (4)
This is the equation of displacement of any particle at a distance x from the origin
where:
y = vertical displacement of vibrating particle, P (m)
Ξ» = Wavelength of wave (m)
A = Amplitude of wave (m)
x = horizontal coordinate of the vibrating particle from the origin (m)
ΞΈ = phase angle (rad)
t = time (s)
T = period (s)
Ο = angular velocity (rad/s)
f = frequency (Hz)
Example 1:
A plane progressive wave is given by the equation π¦ = 2 π ππ (2000ππ‘ β 0.5π₯) Calculate:
(i) Amplitude of the wave
(ii) The frequency
(iii) The wavelength
(iv) The speed and
(v) The period of the wave.
Solution:
By comparing the given equation
π¦ = 2 π ππ (2000ππ‘ β 0.5π₯) with the standard equation
y = A sin (2πππ‘ β 2ππ₯/π)
We have for:
(i) The Amplitude A, of the wave by comparison is 2 m
(ii) The frequency f, of the wave 2πππ‘ = 200 ππ‘
2ft = 2000t
f = 1000Hz
(iii) The wavelength π,
2ππ₯/π = 0.5π₯
2π/π = 0.5
Ξ» = 2Ο/0.5
Ξ» = 12.57m
(iv) The speed v,
v = fΞ» v = 1000 Γ 12.57
v = 12570 m/s
(v) The period T,
T = 1/π
T = 1/1000
T = 0.001 sec.
T = 10-3 s
Example 2:
A wave is represented by the equation π¦ = 2 π ππ (0.5π₯ β 200ππ‘) Calculate:
(i) Amplitude of the wave
(ii) The frequency
(iii) The wavelength
(iv) The speed and
(v) The period of the wave.
Solution:
By comparing the given equation
π¦ = 2π ππ (0.5π₯ β 200ππ‘) with the standard equation
y = A sin (2ππ₯/π β 2πππ‘)
We have for:
(i) The Amplitude A, of the wave by comparison is 2 m
(ii) The frequency f, of the wave
2πππ‘ = 200 ππ‘
2ft = 200 t
f = 100 Hz
(iii) The wavelength Ξ»,
2ππ₯/π = 0.5π₯
2π/π = 0.5
Ξ» = 2ΟΓ2
Ξ» = 12.57m
(iv) The speed v,
v = fΞ»
v = 100 Γ 12.57
v = 1257 m/s
(v) The period T,
T = 1βπ
T = 1/100β
T = 0.01 sec.
T = 10-2 s
Rationale:
Waves are everywhere. Whether we recognize it or not, we encounter waves daily. Sound waves, visible light waves, radio waves, microwaves, water waves, sine waves, cosine waves, stadium waves, earthquake waves, waves on a string, and slinky waves are just a few examples of our daily encounters with waves. waves play a significant role in life because they transfer energy and waves allow for long-range communication via mobile phones, television and radio. sound is waves, pressure waves that travel in air or other fluids or solids. We use sound to hear things, to communicate, and ultrasound (sound too high a frequency to hear) to diagnose illnesses, or to look inside solid materials for flaws, and probably a lot more things. Then there are electromagnetic waves, which are used for radio broadcasting and communications, cellphones, RF remote controls, measuring distances and location (GPS), and even for learning about space by analyzing radio frequency waves coming from galaxies and stars. XRays are radio waves that are just a lot higher frequency. They are called 'ionizing radiation' because they can strip electrons from individual atoms. Light is also a wave (or a particle, depending on how you're talking about it). Light is an electromagnetic wave, like radio waves and X-rays but even higher frequency. Without light, we couldn't see. Also, all the energy that comes to earth is light from the sun, which plants use to make oxygen for us to breathe and food for us to eat. Also, lasers are used for millions of things these days, from surgery to welding metal and plastic, for measuring, communications, targetting munitions, etc. Then there are ocean waves. Useful for surfing.
Prerequisite/ Previous knowledge:
- Newton's Law of Motion
- Physical Wave
Learning Materials:
Demo of water wave, diagram of a wave, tape, string, stopwatches, chart paper, basin, water, guitar, markers.Reference Materials:
- New School Physic for Senior Secondary Schools, by M. W. Anyakowa.
- Lamlas's SSCE and UTME, by O. Ajaja and H. B. Olaniyi
Lesson Development:
STAGE |
TEACHER'S ACTIVITY |
LEARNER'S ACTIVITY |
LEARNING POINTS |
|---|---|---|---|
| INTRODUCTION full class session |
The teacher asks learners to state Newton's first law of motion. | Learners' response to teacher's question. Newton's first law of motion states that every object continues in its state of rest or uniform motion in a straight line unless acted upon by an external force. |
Confirming previous knowledge. |
|
|
|||
| INTRODUCTORY ACTIVITY full class session |
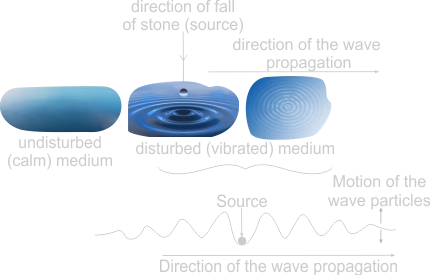
The teacher provides learners with a basin full of water and asks learners the following questions: 1. What is the state of the medium? 2. What is the state of the medium when a stone or a finger is deep into the medium? |
Learners respond to teacher's questions respectively; 1. The media was calm. 2. The media was disturbed, and this led to the generation of ripple/ waves. |
Developing the idea of wave motion. |
| Development 1 |
The teacher tells learners to relate the observation above to define waves in their own words. |
Learners' expected response. 1. A wave is a disturbance which travels outward from its source, carrying energy along with it. 2. Wave motion can also be defined as a process of transferring disturbance (in form of kinetic energy) from one point to another in a medium without any transfer of particles of the media. |
Meaning of wave |
| Stage 2 | Divide students into small groups and provide each group with tape, string, stopwatches, chart paper, and markers. The teacher explains different forms/types of disturbance that generate waves, this includes; Electromagnetic radiation travelling in a vacuum and glass, sound waves travelling through air and water, seismic waves travelling through the Earth. Mechanical disturbance travelling through the string, rope, fluid. The teacher asks learners to define/explain mechanical waves and electromagnetic waves in their own words. |
Learners expected respond. 1. Mechanical waves are those waves that require a material medium for their propagation. Examples of such waves are water waves, sound waves, and waves on a rope or string. 2. Electromagnetic waves are waves that do not require a material medium for propagation. Examples are light waves, radio waves, X-rays and gamma rays. |
Mechanical and Electromagnetic waves. |
|
|
|||
| Stage 3 | The teacher divides students into small groups and provides each group with tape, string, stopwatches, chart paper, basin, water, stone, guitar and markers. The teacher asks learners to state their observations in each activity. The teacher prompts learners to explain stationary waves, progressive waves and the types of progressive (travelling) waves based on their observation of the ACTIVITIES. Stationary wave: Waves which appear to be vibrating vertically without travelling horizontally created from waves with identical frequency and amplitude interfering with one another while travelling in opposite directions. Examples of standing waves are; waves generated by piano, guitar string, two people shaking a jump rope, etc. Progressive Wave: A wave which continues to spread out transferring energy from the source of disturbance is called a progressive wave. Progressive waves have properties such as wavelength, height, amplitude, velocity, frequency, and period. Examples of progressive waves are sound waves, seismic waves, and water waves. |
1. ACTIVITY ONE: The learners use the string to create waves. The learners tape one end of a piece of string (about two feet long) to a desk. The learners pull the string so it is tight, but lays flat against the desk. The learners take turns holding the end of the string and moving it right to left to produce a wave. The learners move the string fast and slow and observed the movement of the wave and draw pictures of the waves they see. 2. ACTIVITY TWO: The learners fill a basin with water and allow the medium to settle/calm, thereafter, dip a finger into the water and observed the disturbance/wave that was generated and the direction of flow/movement of the wave. 3. ACTIVITY THREE: The learners engage in skipping rope exercises and observe the direction and movement of the wave. 4. ACTIVITY FOUR: The learners pluck/strum the guitar string and observed the direction and movement of the wave. The learners state their observations: 1. ACTIVITY ONE: The direction of the disturbance of the wave and the direction of the flow of the wave itself moves in the same direction. 2. ACTIVITY TWO: The direction of the disturbance of the wave and the direction of the flow of the wave itself moves in a different direction. 3. ACTIVITY THREE: There is no direction of flow of the wave, however, there is an up and down movement of the wave. 4. ACTIVITY FOUR: There is no direction of flow of the wave, however, there is an up and down movement of the wave. |
Stationary waves, progressive waves and the types of progressive (travelling) waves. |
| The teacher explains to learners that there are two types of progressive/travelling wave and guide learners to list and explain the types of progressive waves based on the activities above. | Learners are expected to respond. The two types of progressive waves are the Tranverse wave and longitudinal wave. 1. Transverse waves: are waves which travel perpendicularly to the direction of the vibrations producing the waves. That is, a transverse wave is one in which the particle displacements are perpendicular to the direction along which the wave travels. The water wave is a transverse wave since the up-and-down (vertical) motion of the water particles is perpendicular to the direction of wave propagation (horizontal, along the wave surface). Other examples are; light waves, radio waves and wave produced in a rope. 2. A longitudinal wave: is one in which the particle displacements are parallel to the direction along which the wave travels. That is, longitudinal waves are waves which travel in a direction parallel to the vibrations of the medium. The sound wave is an example of a longitudinal wave. |
||
|
|
|||
| Step 4: | The Teacher shows students a diagram of a waves, and various terms use with waves. E.g Crest, Trough, Amplitude, Wavelength, Frequency, etc. The teacher guides learners to explain each of the wave terms above. |
Learners expected answers. 1. Phase: Particles which are at the same verticle distances from their positions of rest and are moving in the same direction are said to be in the same phase. Particles A, C and E are in phase. 2. A Cycle: This is a complete to-and-fro movement or direction of a vibrating particle. 3. Crest: This is the highest point on the wave. 4. Trough: This is the lowest point on the wave. 5. A Node: A node is a point on a stationary wave where there is no movement of the medium. That is a point at which the amplitude of vibration in the standing wave system is zero. The nodes are Ξ»/2 apart. 6. An antinode: Is a point on a stationary wave where there is the maximum displacement of the medium. Antinodes are Ξ»/2 apart. 7. Amplitude (A): This is the maximum displacement of a particle from its resting position. It is measured in metres. 8. Wavelength (Ξ»): This is the distance between two successive crests or successive troughs (or two successive points in phase) of the wave. It is measured in metres. 9. Wavefronts: Can be represented as lines which are always perpendicular to the direction of wave travel. The distance between one wavefront to the next is the wavelength. 10. Frequency (f): This is the number of complete vibrations or cycles that a particle makes in one second. It is also equivalent to the number of complete waves passing at a given point in one second. The S.I unit of frequency is the Hertz (Hz) which is defined as one cycle or oscillation per second (1 cps). The frequency of a wave is identical to the frequency of the source that sends it out. 11. Period (T): This is the time taken by a wave-particle to make one complete oscillation. It is measured in seconds. The period is also the time taken by the wave to travel one wavelength. The period (T) and frequency (f) are related by f = 1/T or T = 1/f 12. Wave Speed or velocity (v): This is the distance the wave travels in one second. Its unit is metre-per-second (m/s) |
Terms used in describing a wave. |
| Step 5 10 mins |
The teacher explains an expression for the Mathematical Relationships between Frequency (f), Wavelength (Ξ») and Velocity (v) and the Mathematical representation of progressive wave motion. Velocity = Frequency x Wavelength v = fΞ» ----------- (1) But f = 1/T Hence v = Ξ»/T Ξ» = vT ----------- (2) The teacher guide learners to derive the mathematical equation of the wave. |
Learners follow the teacher's explanation to derive the mathematical equation of the wave. y = horizontal displacement of the particle from rest at a particular time x = hππππ§πππ‘ππ πππππππππ‘π ππ π‘he π£πππππ‘πππ ππππ‘ππππ, x = A. ΞΈ = oscillation made at a given time one complete oscillation = one wavelength But one complete oscillation = the circumference of circle circumference of circle = 2Ξ©r or 2Ξ©π₯ :. 1π = 1 complete cycle = 3600 = 2Ξ©π₯ Hence, ΞΈ = 2Ξ©π₯/π But sin ΞΈ = y/A y = A sin ΞΈ y = A sin (2Ξ©π₯/π) -------- (1) At t = 0 (at the origin) Where: π΄ = ππππππ‘π’ππ ππ π‘hπ π€ππ£π π = π€ππ£ππππππ‘h ππ π‘hπ π€ππ£π π¦ = π£πππ‘ππππ πππ πππππππππ‘ ππ π‘hπ π€ππ£π π₯ = vππππ§πππ‘ππ πππππππππ‘π ππ π‘hπ π£πππππ‘πππ ππππ‘ππππ The displacement after t seconds is given by: y = A sin (ΞΈ - Ξ¦) y = A sin [2Ξ©/π(π₯2 - π₯1)] But displacement π₯ = velocity v x time t π₯ = vt Let π₯2 = π₯ and π₯1 = vt or π₯2 = vt and π₯1 = π₯ :. y = A sin [2Ξ©/π (π₯ - vt)] y = A sin (2Ξ©π₯/π - 2Ξ©vt/π) But v = πf and π = 2ππ :. y = A sin (2Ξ©π₯/π - 2Ξ©πft/π) y = A sin (2Ξ©π₯/π - 2Ξ©ft) -------- (2) y = A sin (2Ξ©π₯/π - πt) -------- (3) or y = A sin (πt - 2Ξ©π₯/π) -------- (4) This is the equation of displacement of any particle at a distance x from the origin where: y = vertical displacement of vibrating particle, P (m) Ξ» = Wavelength of wave (m) A = Amplitude of wave (m) x = horizontal coordinate of the vibrating particle from the origin (m) ΞΈ = phase angle (rad) t = time (s) T = period (s) Ο = angular velocity (rad/s) f = frequency (Hz) |
Mathematical Relationships between Frequency (f), Wavelength (Ξ») and Velocity (v). Mathematical Representation of Wave Motion - Progressive Wave. |
|
|
|||
| EVALUATION 10 mins |
The teacher asks questions to the learners to evaluate the lesson. 1. Define a wave and explain its significance in physics. 2. Differentiate between mechanical and electromagnetic waves with examples. 3. A wave has a frequency of 60 Hz and travels at a speed of 300 m/s. Calculate its wavelength. 4. If the wavelength of a light wave is 500 nm (nanometers) and it travels at the speed of light (approximately 3 Γ 10βΈ m/s), calculate its frequency. 5. A sound wave has a wavelength of 1.5 m and travels at a speed of 340 m/s. What is its frequency? 6. ........ is the unit of frequency? A) Meter (m) B) Hertz (Hz) C) Joule (J) D) Newton (N) 7. Which of the following statements is true regarding the relationship between wavelength and frequency? A) They are directly proportional. B) They are inversely proportional. C) They are unrelated. D) They are both measured in the same unit. 8. What type of wave requires a medium to travel through? A) Electromagnetic wave B) Sound wave C) Light wave D) Radio wave |
The learners answer the teacher's questions. 1. A wave is a disturbance that transfers energy from one place to another without transferring matter. Waves are significant as they explain various physical phenomena such as sound, light, and seismic activities. 2. Mechanical waves require a medium to travel (e.g., sound waves), while electromagnetic waves do not require a medium (e.g., light waves). 3. Wavelength Calculation: Given: Frequency = 60 Hz, Speed = 300 m/s Wavelength (Ξ»): Ξ» = v/f Ξ» = 300/60 Ξ» = 5m 4. Frequency Calculation for Light Wave: Given: Wavelength Ξ» = 500 nm Ξ» = 500 Γ 10β»βΉ m, Speed of light c = 3 Γ 10βΈ m/s Frequency (f): f = c/Ξ» f = 3 Γ 10βΈ m/s / 500 Γ 10β»βΉ m f = 6 Γ 10ΒΉβ΄Hz 5. Frequency Calculation for Sound Wave: Given: Wavelength = 1.5 m, Speed = 340 m/s Frequency (f): f = v/Ξ» f = 340/1.5 f β 226.67Hz 6. B) Hertz (Hz) 7. B) They are inversely proportional. 8. B) Sound wave |
Ask the learners questions to assess the achievement of the set objectives. |
| CONCLUSION 2mins |
1. If the frequency of waveform A is 60 Hz, what is the period of waveform B? 2. What is the number of type-B waves passing a given point in the medium in 5 sec? 3. If the speed of the waves is 5 m/s, calculate the distance between two successive particles of waveform-A which are in phase. |
Learners conclude the lesson. 1. Period of A = 1/60 sec Period of B = 3/2 x period of A Period of B = 3/2 x 1/60 Period of B = 1/40 sec, or 0.025 sec. 2. Frequency of B = 0.025 = 40 Hz, i.e. 40 waves pass any given point in one second, or 200 waves in 5 sec. 3. The required distance is the wavelength Ξ» = v/f Therefore, the wavelength = (500/60)cm, or 8.33cm. |
Application: calculation of the wave concept. |
|
|
|||
| ASSIGNMENT | The teacher gives learners a take home. | 1. A vibrating plate is used to generate waves in a pool of water. The distance between successive troughs is 7cm and a crest travels from the vibrator to the edge of the pool, 52.5cm away, in 2.5 sec. Calculate the frequency of the vibrator. 2. A rarefaction and an adjacent compression of a sound wave travelling in the air are separated by a distance of 15cm. If the velocity of sound in air is 330 m/s. What is the frequency? 3. If the speed of sound in air is 340 m/s, what is the period of vibration of sound waves of wavelength 1.7m? 4. Which of the following phenomena does not apply to longitudinal waves? β’ interference β’ refraction β’ diffraction β’ polarization 5. Which of the following waves is both mechanical and transverse? β’ radio β’ sound β’ water β’ x-rays 6. What is the frequency of a wave having a wavelength of 20cm and a velocity of 0.5 m/s? 7. An anchored boat is hit by water crests every 5sec. If the wave crests are 60m apart, What is the velocity of the wave? 8. (a) What is wave motion? (b) The equation: y = A sin 2π/π(π£π‘ β π₯) represents a wave train in which y is the vertical displacement of a particle at a distance x from the origin in the medium through which the wave travelling. Explain, with the aid of a diagram, what A and Ξ» represents. 9. A radio waves transmitted from a certain radio station is represented by the wave equation: π¦ = 0.75 sin (0.67 ππ₯ β 2 Γ 108 ππ‘) Calculate the; (i) wavelength of the wave (ii) frequency of the wave (ii) velocity of the wave. Where x, y are in meters while t is in seconds. 9. What is wave? 10. Elias radio station broadcasts at a frequency of 21MHz. If the speed of light in the air 3Γ108ms-1, calculate the wavelength of the broadcast. 11. Define stationary wave. 12. An electromagnetic radiation has a speed of 3Γ108ms-1 and a frequency of 106Hz, calculate its wavelength (a) 3.3Γ103 m (b) 3.0Γ102 m (c) 3.0Γ10-2 m (d) 3.3Γ108 m (e) 3.3Γ10-3 m 13. A body oscillates in simple harmonic motion according to the equation π₯ = 0.05 cos(3π + π/3) where x is expressed in meters. What does 0.05 represents? (a) velocity (b) frequency (c) period (d) amplitude (e) none of the above 14. Which of the following is not a mechanical wave? (a) wave propagated in stretched string (b) waves in a closed pipe (c) radio waves (d) water waves (e) sound waves 15. The maximum displacement of particles of wave from their equilibrium positions is called. (a) wave velocity (b) period (c) amplitude (d) wavelength (e) frequency (a) 20Hz (b) 10 Hz (c) 5 Hz (d) 4 Hz (e) 50 Hz |
Improving their level of understanding of waves. |