Lesson Plan and Lesson note on Physics
Nucleus & Radioactivity
Subject: Physics
Theme: Energy Quantization And Duality Of Matter
Topic: Nucleus
Sub Topic: Radioactivity
Date: dd/mm/yyyy
Class: S.S 3
Average Age: 16 years and above
Duration: 40 Minutes
No of Learners: 40
At the end of the lesson, the students should be able to:
1. Explain the ATOMIC STRUCTURE AND CHEMICAL BEHAVIOUR
Today we consider the atom as made up of tiny but massive nucleus at the centre and outside the nucleus (singular - nucleus, plural - nuclei) is a cloud of electrons which move in wave-like orbits or shells around the massive nucleus. The nucleus consists of protons which carry positive changes and neutrons which carry no charge. The neutron and proton together constitute the nucleon. All the mass of an atom is concentrated in the central nucleus. The protons, neutrons and electrons are the fundamental sub atomic particles of the atom.The electron is the lightest particle of an atom, with a mass (Me) of 9 × 10-31 kg and an electronic charge e- = 1.6 × 10-19 C.
The proton has a mass of 1.67 × 10-27 kg which is over 1836 times heavier than the mass of an electron. It carries a positive charge, e+ = 1.67 × 10-29 C ( i.e e+ = e- = 1.6 × 10-10). There are the same number of protons in the atoms of different elements.in a neutral atom, the number of protons equals the number of electrons. We denote the atom of an element × by AzX
A = mass number
Z = atomic number
The atomic number or proton number (Z) is the number of protons in the nucleus of an element. The mass number or nucleon number (A) is the total number of protons and neutrons in an atom of an element
2. Explain the Nucleus of an Atom
The nucleus of an atom is the central region of an atom where the majority of the mass is concentrated. Through the scattering of alpha particles experiment by Rutherford, we learned that the nucleus of an atom contains a majority of the mass of the atom. Numerically speaking, the nucleus of an atom occupies almost 10-14 times the volume of the atom but contains 99.99% of the atomic mass. The nucleus of an atom is so small that if you expanded an atom to fill up a room, the nucleus of an atom would still be no larger than a pinhead!
Nucleus of an Atom - atomic mass
An atom is tiny and therefore its mass is also proportionally minute. A regular unit of mass such as a Kilogram (Kg) cannot be used to weigh something as small as an atom and to address this issue, scientists have created a new unit of mass. It is called the Atomic Mass Unit (u). Its reference is taken as Carbon-12 and 1 Atomic Mass unit is equal to 1/12th the weight of one atom of Carbon 12.
1 u = one atom of 1/12 of C-121 u = 1/12 kg of 1.992647 × 10-26
1 u = 1.660539 10-27 kg
This is the mass of a hydrogen atom! Surprisingly except for a few elements, most of them are whole multiples of the weight of the Hydrogen atom.
Nucleus of an Atom - Composition
The Nucleus of an atom consists of a tightly packed arrangement of protons and neutrons. These are the two heavy particles in an atom and hence 99.9% of the mass is concentrated in the nucleus. Of the two, the protons possess a net positive charge and hence the nucleus of an atom is positively charged on the whole and the negatively charged electrons revolve around the central nucleus. Since the mass concentration at the nucleus of an atom is immense the nuclear forces holding the protons and the neutrons together are also large. The protons are in such close vicinity to each other inside the tiny nucleus and therefore the electrostatic forces of repulsion also act inside the nucleus. Nuclear energy relies on nothing but releasing the energy trapped in the nucleus of an atom. The total number of protons in a nucleus is equal to the number of electrons revolving around the nucleus and hence the atom, on the whole, is electrically neutral.
understand how the nuclear forces have changed the face of both the earth and war. The creation of nuclear weapons proved that we had understood the workings of the atom.3. Defined Radioactivity
Radioactivity basically refers to the particles which are emitted from nuclei as a result of nuclear instability.Due to nuclear instability, an atom’s nucleus exhibits the phenomenon of Radioactivity. Energy is lost due to radiation that is emitted out of the unstable nucleus of an atom. Two forces, namely the force of repulsion that is electrostatic and the powerful forces of attraction of the nucleus, keep the nucleus together. These two forces are considered extremely strong in the natural environment. The chance of encountering instability increases as the size of the nucleus increases because the mass of the nucleus becomes a lot when concentrated. That’s the reason why atoms of Plutonium, Uranium are extremely unstable and undergo the phenomenon of radioactivity.
Henry Becquerel discovered radioactivity by accident. A Uranium compound was placed in a drawer containing photographic plates, wrapped in a black paper. When the plates were examined later, it was found that they were exposed! This exposure gave rise to the concept of Radioactive decay.
Hence, the SI unit of radioactivity is becquerel (Bq) and this term is named after Henri Becquerel.
Unit of radioactivity is defined as: The activity of a quantity of radioactive material where one decay takes place per second.
1 becquerel = 1 radioactive decay per second
Other Radioactivity Units
There are usually three radioactivity units. An older radioactivity unit is the curie (Ci) and the name has been taken from Pierre and Marie Curie.
- It is defined as that quantity of any radioactive substance which gives 3.7 × 1010s-1 disintegration per second (dps).
- Sometimes millicurie (mc) and microcurie (mc) are also used.
Another unit is Rutherford (rd) and it is defined as the amount of radioactive substance which gives 106 disintegrations per second (dps).
1 curie = 3.7x1010 radioactive decays per second1 becquerel = 1 radioactive decay per second = 2.703x10-11 Ci.
1 rutherford = 1.106 radionuclide decays per second
4. List and explain types of Radioactivity
There are two types of radioactivity1. Natural radioactivity
2. Artificial radioactivity
1. Natural radioactivity
Natural radioactivity is the spontaneous disintegration of the nucleus of an atom during which Alpha(α) particles, Beta(β) particles or Gamma(γ) rays and heat (or energy) are released. When a radioactive elements undergoes radioactive decay, it may emit either α ,B, or γ rays. This changes the atomic number of the element, hence a new element is formed.(i) 22688X α→ 42He + 22286Rn + energy
(ii) 22288 2β→ 2(0-1e) + 22290Ra + energy
(iii) 23892U 2α, 2β→ 2(42He) + 2(0-1e) + 23091Th + energy
(iv) 23490U β→ 0-1e + 23491Pa + energy
Generally we represent alpha (α), Beta(β) and Gamma(γ) decay respectively by
AZX → A-4Z-2Y + 42He
AZX → AZ+1Y + 0-1e
AZX → AZY + 00Y
Example,
alpha (α) decay
23892U → 23490Th + 42He
beta (β) decay
13153I → 13154Xe + 0-1e
beta (β) positron decay as
116C → 115B + 01e
Gamma (γ) decay
23490Th → 23490Th + 00γ
2. Artificial radioactivity
If the radioactivity is induced in an element by irradiation with for neutrons, the process is known as artificial radioactivity. By irradiation, it means exposure to radiation either by accident or by intent.42He + 147N → 189F 178O + 11H + energy
in artificial radioactivity, an ordinary materials is made radioactive by bombarding itwith radioactive particles.
4He + 27Al → 30P + 1n
10n + 63Li → 31H + 42He + energy
10n + 2412Mg → 2411Na + 11P + energy
42He + 94Be → 126C + 10n + energy
10n + 5927Co → 6027Co + energy
Isotopes can also be made artificially by bombarding neutrons, or protons or deuterons at elements e.g.
3410S + 10n → 3510S + energy
7910Br + 10n → 3510Br + energy
such artificially produced isotope are unstable and decay with the emission of α – particles, β –particles and γ – rays. They are called radio isotopes.
5. Explain Isotopes
Isotopes are atoms of the same element which have the same atomic number (X) but different mass number. Isotopes are thus atoms with the same number of protons, but different number of neutrons. Isotopes have similar chemical properties because they have the same number of electrons round the nucleus. Chemical combinations is due to an exchange of outer or valence electrons between elements.Examples of isotopes
a) i. 3517Cl (17 protons , 17 electrons, 18 neutrons)
ii. 3717Cl (17 protons, 17 electrons, 20 neutrons)
b) 126Cl (6 protons, 6 electrons, 6 neutrons)
136Cl (6 protons, 6 electrons, 7 neutrons)
c) 168O (8 protons, 8 electron 8 neutrons)
178O (8 protons, 8 electrons, 9 neutrons)
188O (8 protons, 8 electrons, 10 neutrons)
d) 23892U (92 protons, 92 electrons, 146 neutrons)
238\592U (92 protons, 92 electrons, 143 neutrons)
23492U (92 protons, 92 electrons, 142 neutrons)
Some isotopes are stable, while others are radioactive. For example, carbon-12 (12C) is stable, while carbon-14 (14C) is radioactive.
6. Explain Radioactive Elements:
Radioactive elements are elements that have unstable nuclei and undergo radioactive decay. These elements can exist in various isotopes, with some being stable and others radioactive. Common radioactive elements include uranium-235 (235U), thorium-232 (232Th), radium-226 (226Ra), radon and polonium.These are elements that undergo naturally disintegration spontaneously emit radiation and particles to produce new elements. They tend to stabilise by ejecting particles and emitting energy.
7. Explain Radioactive Emission
Radioactive emission involves the release of particles and radiation from the nucleus of a radioactive atom. These emitted particles or radiations according to Rutherford, are alpha particles, beta particles and gamma radiation. The nuclei of these elements spontaneously emit radiation, which is energy in the form of particles or waves and can undergo radioactive decay.Alpha Decay:
Alpha particles (α) consist of two protons and two neutrons and are positively charged. In alpha decay, an unstable nucleus emits an alpha particle, reducing its atomic number by 2 and its mass number by 4.Beta Decay:
Beta particles (β) are either electrons (β-) or positrons (β+). In beta decay, a neutron is transformed into a proton (β-) or vice versa (β+), and a beta particle is emitted. This changes the atomic number while keeping the mass number constant.Gamma Radiation:
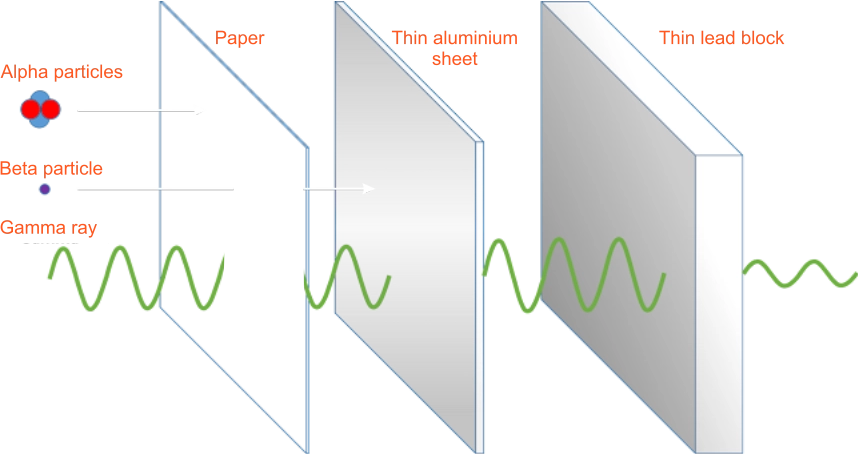
Gamma rays (γ) are electromagnetic radiation (high-energy photons) emitted from the nucleus. They do not affect the atomic number or mass number but can be highly penetrating.| Radiation | Alpha-particles | Beta Particles | Gamma–rays |
|---|---|---|---|
| Nature | Helium nuclei 42He | High Energy electrons | Electromagnetic wave of short wavelength |
| Velocity | 5 – 7% speed of light | Travel at approx. speed of light | Travel at speed of light |
| Effects of magnetic field | Slightly deflected in a magnetic field (+ve) | Strongly deflected in a magnetic field (-ve) | No effects |
| Ionizing magnetic field | Large, cause heavy ionization | Medium | Small |
| Penetrating power | Little penetrating power e.g thin sheet | Good penetrating power e.g aluminium | High penetrating power e.g leads |
8. Explain Half-Life and Decay Constant
(i) Half-Life:
The half-life (T1/2) of a radioactive substance is the time it takes for half of a sample of that substance to decay. It is a characteristic property of each radioactive isotope and is used to measure the rate of radioactive decay.The rate of decay of radioactive elements is found to be proportional to the number of atoms of the material present. If there are N atoms of a radioactive element present at a time, t1, then the probable number of disintegration per unit time or activity.
N α -(dN)/(dt)
The minus sign arises from the fact that N is decreasing with time.
(dN)/(dt) = -λN
λ is a constant of proportionality called the decay constant.
:. λ = - (1/N){dN/dt}
Hence, decay constant is defined as the instantaneous rate of decay per unit atom of a substance.
λ = No of atoms disintegrating per second ÷ No of atoms in the source at that time
By integration
N = Noe-λt
Where
No = Number of atoms present at time t = o
N = Number of atoms present at time t
T = 0.693 ÷ λ
(ii) Decay Constant (λ):
The decay constant λ, (lambda) is a measure of how quickly a radioactive substance decays. It is related to the half-life by the equationλ = ln(2) ÷ T1/2
where ln(2) = 0.632 is the natural logarithm of 2. The concept of half-life is essential for understanding how long it takes for a given amount of a radioactive substance to decay and for various applications, such as radiometric dating and medical imaging using radioactive tracers.
E.g
The amount of radioactive material, A, compared to the original amount Ao or any quatity which is proportional to the radioactive material, A, is
A = Ao2-t/T1/2
A = Aoe-0.693t/T1/2
-
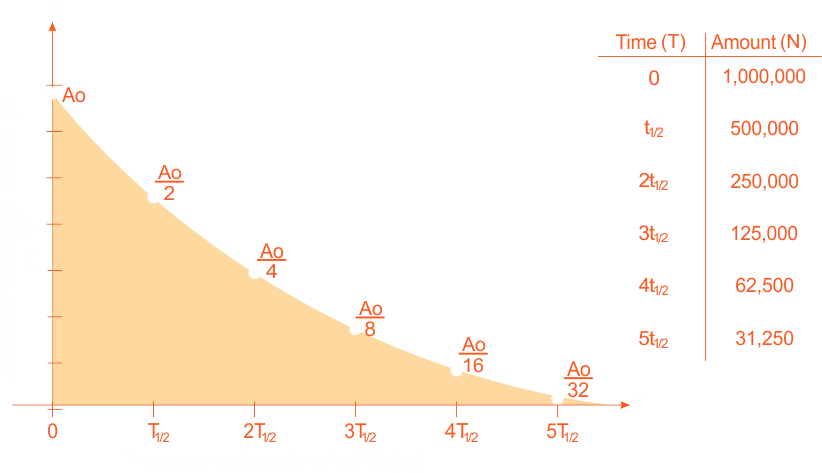Amount of radioactive material (A) compared to the original amount Ao or any quantity which is proportional to A.
(iii) Decay Rate or Activity of Substance (Ao)
The Decay rate is given by the equation Ao = λNwhere λ is the decay constant
No is the number of radioactive nuclei.
Ao = Activity of the substance
(iV) Radioactive dating
This is an application of radioactive decay in which the age of a material is determined by the amount of radioactivity of a particular type that occurs. Its most famous application is carbon-14 dating. Carbon-14 has a half-life of 5730 years and is produced in a nuclear reaction induced when solar neutrinos strike 14N in the atmosphere.Thus, if you know the number of carbon nuclei in an object (perhaps determined by mass and Avogadro’s number), you multiply that number by 1.3×10−12 to find the number of 14C nuclei in the object. When an organism dies, carbon exchange with the environment ceases, and 14C is not replenished as it decays. By comparing the abundance of 14C in an artifact, such as mummy wrappings, with the normal abundance in living tissue, it is possible to determine the artifact’s age (or time since death). Carbon-14 dating can be used for biological tissues as old as 50 or 60 thousand years, but is most accurate for younger samples, since the abundance of 14C nuclei in them is greater. Very old biological materials contain no 14C at all. There are instances in which the date of an artifact can be determined by other means, such as historical knowledge or tree-ring counting. These cross-references have confirmed the validity of carbon-14 dating and permitted us to calibrate the technique as well. Carbon-14 dating revolutionized parts of archaeology and is of such importance that it earned the 1960 Nobel Prize in chemistry for its developer, the American chemist Willard Libby (1908–1980).
There are other forms of radioactive dating. Rocks, for example, can sometimes be dated based on the decay of 238U. The decay series for 238U ends with 206Pb, so that the ratio of these nuclides in a rock is an indication of how long it has been since the rock solidified. The original composition of the rock, such as the absence of lead, must be known with some confidence. However, as with carbon-14 dating , the technique can be verified by a consistent body of knowledge. Since 238U has a half-life of 4.5×109y, it is useful for dating only very old materials, showing, for example, that the oldest rocks on Earth solidified about 3.5×109 years ago.
Example 1.
A certain radioactive element has a half-life of 10 years. (i) How long will take to lose 7/8 of its atoms originally present.
(ii) How long will it take until only ¼ of the atoms originally present remain unchanged.
Solution
(i) T1/2 = 10 years
If 7/8 of its atoms has been lost,
then N - 7N/8 = N/8 atoms remains
But Ao = 0 year
Ao/2 = 10 years
Ao/2 × 1/2 = 20 years
Ao/4 × 1/2 = 30 years
i.e Ao/8 = N/8 atoms remains
:. it takes 30 years to lose 7/8 of its atoms
(ii) N atoms remain unchanged after 0 years
N/2 remain unchanged after 10 years
N/4 remains unchanged after 20 years
Example 2.
The half-life of a radioactive substance is 14 days. If 48g of this substance is stored, after how many days will 1.5g of the original substance remain?
SOLUTION
Using N = No × (1/2)n
No = 48g,
N =1.5g
n = number of half-lives
1.5 = 48 × (1/2)n
But 1.5 = 15/10, 15/10 = 3/2
:. 3/2 = 48 × (1/2)n
3/2 × 1/48 = (1/2)n
3/96 = (1/2)n
1/32 = (1/2)n
(1/2)5 = (1/2)n (same base, equate power)
:. n = 5
Total time = n × t1/2
Total time = 5 × 14 = 70 days
Therefore, 1.5g will remain after 70 days.
Example 3.
The half-life of strontium-90, 9038Sr, is 28.8 years. [One mole of 9038Sr is 89.91 g, Avogadro’s number (NA) = 6.022×1023 atoms/mol] Find;
(a) its decay constant and
(b) the initial activity i.e decay rate of 1.00 g of the material.
SOLUTION
(a) T1/2 = 28.8 yrs
But 1 year = (60 × 60 × 24 × 366)secs
28.8 yrs = 28.8 × 3.16 × 107s
T1/2
= 9.1 × 108
But Decay constant λ = ln(2)/T1/2
λ = 0.693/T1/2
λ = 0.693/9.1 × 108
λ = 7.61 × 10−10s−1
(b) We find the initial number of nuclei in 1.00 g of the material
number of nuclei = atomic mass in 1.00g × Avogadro’s number
number of nuclei in 1.00 g = (1.00g ÷ 89.91g/mol) × Avogadro’s number
number of nuclei in 1.00 g = 1/89.91 × 6.022×1023 nuclei
number of nuclei in 1.00 g = 6.70 × 1021 nuclei
:. Decay rate (Ao) in 1.00 g = Decay constant (λ) × Number of nuclei (No) in 1.00 g
Ao = λNo
Ao = (7.61 × 10−10s−1)(6.70 × 1021 nuclei)
Ao = 5.10 × 1012decays/s.
Example 4.
Approximately 20% of the human body by mass is carbon. Calculate the decay rate due to 14C in 1.00 kg of carbon found in a living organism. Express the decay rate in units of Bq and Ci.
[One mole of Carbon-14 = 12.0g since it is nearly pure 12C, half-life of Carbon-14 = 5730 yrs, abundance of 14C in a carbon sample from a living organism = 1.3 × 10−12, Avogadro’s number = 6.022×1023 atoms/mol]
N/B: If you know the number of carbon nuclei in an object, you multiply that number by 1.3×10−12 to find the number of 14C nuclei in that object.
SOLUTION
1.00kg of carbon = 1000g of carbon
number of carbon-12 nuclei (No) in 1000g = atomic mass in 1000g × Avogadro’s number
No of 12C = 1000g/12.0gmol-1 × 6.022×1023
No of 12C = 5.02×1025
:. No of 14C = 5.02×1025 × 1.3 × 10−12
No of 14C = 6.52 × 1013
λ = 0.693/T1/2
λ = 0.693/5730
λ = 1.2×10−4
Hence, decay rate Ao = λN
Ao = 1.2×10−4 × 6.52 × 1013
Ao = 7.8×109y−1
(i)To convert 7.8×109y−1 to the unit Bq
But 1 year = (60 × 60 × 24 × 366)secs
7.8×109 years = 7.8×109 × 3.16 × 107s
2.4648×1017 = 250Bq
(ii) To covert 250Bq to the unit Ci
1 Bq = 2.703×10-11 Ci.
250Bq = 250 × 2.703×10-11 = 6.76nCi
EXAMPLE 5.
In an ancient burial cave, your team of archaeologists discovers ancient wood furniture. Only 80% of the original 14C remains in the wood. How old is the furniture?
[half-life of 14C is 5730y] SOLUTION
N/No = e−λt
Where,
N - total number of radioactive nuclei remaining after time t
No = original number of nuclei at t = 0
λ = 0.693/T1/2
λ = 0.693/5730
λ = 1.2 × 10-4
The problem statement implies that N/No = 0.80
N/No = 0.80
0.80 = e−λt
ln0.80 = −λt
−0.223 = −λt
t = 0.223/λ
t = 0.223/1.2 × 10-4
t = 1844y
The furniture is almost 2000 years old—an impressive discovery. The typical uncertainty on carbon-14 dating is about 5%, so the furniture is anywhere between 1750 and 1950 years old. This date range must be confirmed by other evidence, such as historical records.
9. Explain Nuclear Reaction & Artificial transformation
Nuclear Reaction is the spontaneous emission of radiation that involves the nuclei of radioactive element.Artificial transformation is induced in an element by irradiation (exposure to radiation) either by accident or by intent) . It was first achieved by Rutherford. An ordinary material not normally radioactive is made radioactive by bombarding it with radioactive particles e.g
42He + 2713Al → 3015P + 10n
(i) Nuclear Energy
The protons and neutrons (nucleons) in the nucleus of each atom are held together by very powerful nuclear forces. An enormous amount of energy is required to tear the nucleon apart. Enrico Fermi (1934) discovered that the nucleus can be split by bombarding it with a slow neutron.He discovered that the total mass of the component products is less than the mass of the original materials. The difference in mass (mass defect) is a measured of the nuclear energy released. According to Albert Einstein
E = Δmc2
E = nuclear energy
Δm = mass defect
c = velocity of light (3.0 × 108ms-1)
(ii) Nuclear fusion
From the word fuse, this is the process in which two or more light nuclei of elements combine together to form a heavier nucleus with the release of both energy and radiation. This process is used to produce a hydrogen bomb; it is also believed to be the source of energy of the sun and stars.To bring the two lights nuclei together in a fusion process, very high temperature of the order 10,6000C are required to overcome the coulomb repulsive forces between the two nuclei. E.g
21H + 31H → 41He + 10n + energy.
-
Neutron Induced Fusion
(iii) Nuclear fission
This is the process in which the nucleus of a heavy element is split into two approximate equal parts with the release of a huge amount of energy and neutrons. The process is used to produce an atomic bomb.Fission occurs with most of the massive nuclei. When the heavy nucleus is bombarded by slow neutron, several neutrons are produced as by–products.
These neutrons may cause the splitting of other nuclei, which in turn yield more neutrons which may further split other nuclei and so on. Thus a chain reaction is set in motion.
10n + 23592U → 14156Ba + 9236Kr + 310n + energy.
-
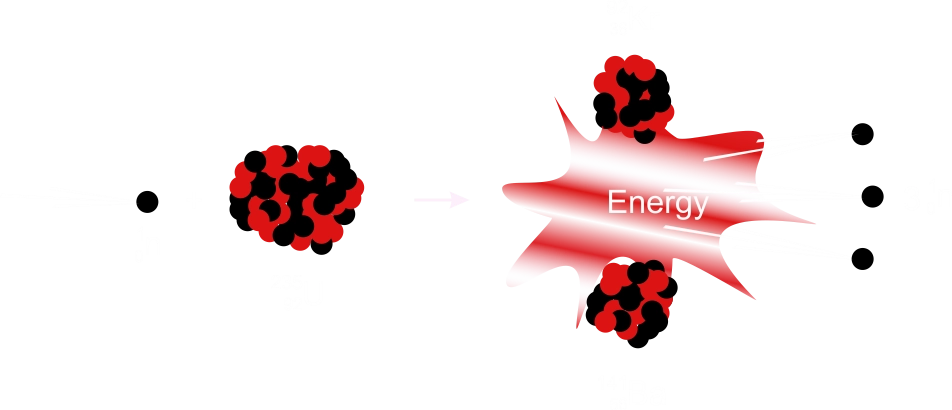Neutron Induced Fission
(iv) Chain Reaction
A chain reaction is a multiplying and self maintaining reaction. When the size of the nuclei exceeds a certain critical mass, there is a rapid production of neutron accompanied by a release of tremendous amount of energy in a nuclear explosion. This is the principle of the atomic and nuclear fission bombs. It is also the process used in the present day nuclear power station.10. Explain Advantages of fusion over fission
1. Fusion is more easily achieved with lightest element e,g hydrogen.2. The raw materials required from fusion are more readily and cheaply available.
3. Fusion process produces less dangerous by-products.
11. Explain Peaceful uses of nuclear energy
1. Many nuclear power plants are now being used to generate electricity.2. Several fission products obtained in nuclear reaction are used for radiotherapy.
3. Radio isotopes from nuclear plants are used in agriculture as tracers and preservatives.
4. some space crafts. Ships and submarines are powered by nuclear energy.
12. Explain Applications of Radioactivity
Radioactivity has many applications, including:1) Medical imaging: Radioactive isotopes can be used to create images of the inside of the body. This is used to diagnose and treat diseases.
2) Food preservation: Radioactive isotopes can be used to kill bacteria and other microorganisms in food. This helps to prevent foodborne illness.
3) Industrial applications: Radioactive isotopes can be used to measure the thickness of materials, to sterilize medical equipment, and to create glow-in-the-dark paints.
4) Nuclear power plants use nuclear fission to generate electricity.
13. Explain Nigeria Nuclear Energy Programme
Nigeria is currently developing a nuclear energy programme. The programme aims to build a nuclear power plant to generate electricity. The government of Nigeria has signed agreements with Russia and China to help with the development of the programme.Nigeria's nuclear energy programme is still in its early stages, but the government has ambitious plans to build four nuclear power plants by 2030. The programme is being led by the Nigeria Atomic Energy Commission (NAEC) and the Nigerian Nuclear Regulatory Authority (NNRA).
The NAEC was established in 1976 to promote and develop the peaceful uses of nuclear energy in Nigeria. The NNRA was established in 1995 to regulate the nuclear industry in Nigeria.
The government of Nigeria has signed agreements with Russia and China to help with the development of the nuclear energy programme. Russia is providing technical assistance and training for the NAEC, while China is providing financing for the construction of the nuclear power plants.
The first nuclear power plant is planned to be built in the Taraba State in northeastern Nigeria. The plant is expected to have a capacity of 1,000 megawatts (MW). The other three plants are also expected to have a capacity of 1,000 MW each.
The construction of the nuclear power plants is expected to cost an estimated $10 billion. The government of Nigeria is planning to finance the construction through a combination of loans and equity investment.
The nuclear energy programme has been met with some opposition from environmental groups and local communities. These groups are concerned about the safety of nuclear power plants and the potential environmental impacts of nuclear waste.
The government of Nigeria has assured the public that the nuclear energy programme will be safe and environmentally sound. The government has also said that it will consult with local communities before the construction of the nuclear power plants.
The development of Nigeria's nuclear energy programme is a significant step for the country. Nuclear energy has the potential to provide a clean and reliable source of electricity for Nigeria. However, the programme also faces some challenges, and it is important to ensure that it is implemented safely and responsibly.
Here are some of the challenges that Nigeria's nuclear energy programme faces:
(i) Financial constraints: The construction of nuclear power plants is a very expensive undertaking. The government of Nigeria will need to secure funding for the programme.
(ii) Technical expertise: Nigeria does not have a strong nuclear industry. The government will need to develop the technical expertise to build and operate nuclear power plants.
(iii) Public acceptance: There is some opposition to the nuclear energy programme from environmental groups and local communities. The government will need to address these concerns in order to gain public acceptance for the programme.
Despite these challenges, Nigeria's nuclear energy programme has the potential to be a success. Nuclear energy can provide a clean and reliable source of electricity for Nigeria, and it can help to diversify the country's energy mix. The government of Nigeria will need to carefully address the challenges facing the programme in order to ensure its success.
Rationale:
In order to understand the various chemical reactions that occur around us and the parameters governing these reactions, we need an understanding of the elements and compounds taking part in these reactions. The early developments in science revealed that matter is made up of atoms which in turn are composed of elementary particles known as electrons, protons and neutrons. In order to have a better understanding of the transformations of matter from one form to the other, scientists needed a defined structure for an atom and its interaction with other atoms.Prerequisite/ Previous knowledge:
Photoelectric Effect.Learning Resources:
Flash cards, an audio and video youtube examples, Available useful objects.A chart showing deflection of particles in a magnetic and electeric field
Reference Materials:
1. New system physics for secondary school by Dr. Charles chew etal2. New school physics by M. W Anyakoha
3. Internet facility
Lesson Development:
STAGE |
TEACHER'S ACTIVITY |
LEARNER'S ACTIVITY |
LEARNING POINTS |
|---|---|---|---|
| STEP 1: INTRODUCTION Individual Student |
The teacher asks the students the following question: What do you understand by the nucleus of an atom? |
The students expected answers: An atom is divided into two (2) parts; the nucleus and the electron. The nucleus contains two basic particles: The proton, which is positively charged. The neutron, which is neutral The Proton (Atomic Number Z)This is the total number of protons in the nucleus of an atom. Proton number determines the properties of the element. All elements with the same proton number have the same chemical properties.Nucleon (Mass Number A)This is the total number of protons and neutrons in the nucleus of an atom. For a nuclide of mass or nucleon number (A) and atomic or proton number (Z), the total number of neutrons in the nucleus is given by: n = A-Z. Where n is the number of neutrons in the nucleus of the atom. |
Identification of Prior Ideas and revising previous lesson |
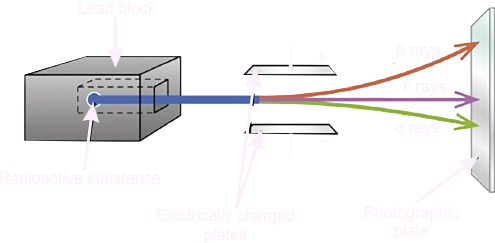
| STEP 2: Development and Grouping |
The teacher asks students to form groups and choose their leaders and secretaries. Thereafter, the teacher’s leads the students to understand that if a small sample of radium is placed at the bottom of a small hole drilled in a block of lead. The radiation emitted from this radium emerged from the hole in a narrow beam. if the rays were subjected to a strong magnetic field placed at the side of a beam. A photographic plate situated at appropriate sides to receive the rays showed that the paths of some rays were bent to the right, some to the left and some went straight on, unbent. Electrically charged plates placed at the side of the beam gave the same effect. The radiations that was bent towards the negative electric plate or the south pole of the magnetic field are called the Alpha particles (α –particles). The radiations deflected towards the positive electric plate or the North pole of the magnetic field is called Beta particles (β – particles). The radiation that was neither affected by the electric or magnetic field is called gamma rays (γ). They are actually electromagnetic radiations. Radioactivity is a spontaneous decay of unstable nuclei with the release of energy and radiation such as alpha particle, Beta particle and gamma ray. This is the spontaneous emission of radiation by radioactive element such as Thorium, Uranium etc. Radioactive elements are elements that undergo disintegration spontaneously emit radiation and particles. Example include; radon, radium, uranium and polonium. A form of radioactivity which occur spontaneously without doing anything to initiate it nor can anything be done to control it is called NATURAL radioactivity. A form of radioactivity that is induced in element that would have otherwise being stable is called induced or ARTIFICIAL radioactivity Characteristics of radioactivity 1. Spontaneously and continually emitting of radiation by radioactive element. 2. Temperature and pressure have no effect on radioactivity. 3. The radiation can pass through opaque objects. 4. It affects photographic plates. 5. It causes ionization of gases through which it passes. 6. It causes fluorescence of certain substance. 7. It releases large amount of energy. |
The students form groups and choose their leaders and secretaries. The students write down what the teacher explains and listen attentively. |
Inculcating leadership skills, competitive spirit, cooperation, teamwork and a sense of responsibility among learners. Develping the Concept of the topic Radioactivity |
|
| |||
| STEP 3: EXPLORATION Entire Class |
The teacher’s leads the students to understand Difference between natural and artificial radioactivityNatural Radioactivity1. It is spontaneous disintegration of a radioactive substance2. It involves heavy nuclei 3. It involves unstable nuclei Examples of natural radioactivity (i) 23492U → 23090Th + 42He + ΔE (ii) 23090Th → 22688Ra + 42He + ΔE (iii) 22688Ra → 22286Rn + 42He + ΔE (iv) 22286Rn → 19884Po + 42He + ΔE Artificial Radioactivity1. It is an induced disintegration of a nucleus by bombardfing it with a particle2. It involes stable nuclei 3. It involves light and stable nuclei Example of Artificial Radioactivity (i) 42He + 147N → 178O + 11H + ΔE (ii) 11H + 73Li → 242He + ΔE (iii) 10n + 63Li → 42He + 31He + ΔE |
The students write down what the teacher explains and listen attentively. | Difference between natural and artificial radioactivity. |
| STEP 4: DISCUSSION Entire class |
The teacher leads the students to defined Isotopes | The students Respond to the teachers question Isotopes are atoms of the same element with the same number of protons but differ in the number of neutrons i.e. isotopes have the same atomic (proton) number but different mass (nucleon) numbers. For example, hydrogen 11H, deuterium 21H, and tritium 31H. The number of protons in the nucleus of an atom is called the atomic number, and it determines the element of the atom. The number of neutrons is called the neutron number. |
Isotopes |
| The teacher explains Radioactive Elements with the students. Radioactive elements are the elements that naturally disintegrate on their own to produce new elements. Radioactive elements are heavy and unstable. They tend to stabilise by ejecting particles and emitting energy. These emitted particles or radiations according to Rutherford, are alpha particles, beta particles and gamma radiation. The nuclei of these elements spontaneously emit radiation, which is energy in the form of particles or waves and can undergo radioactive decay. |
The students listen and write down. | Radioactive Elements | |
|
| |||
The teacher use the chart to explain properties of radioactive radiations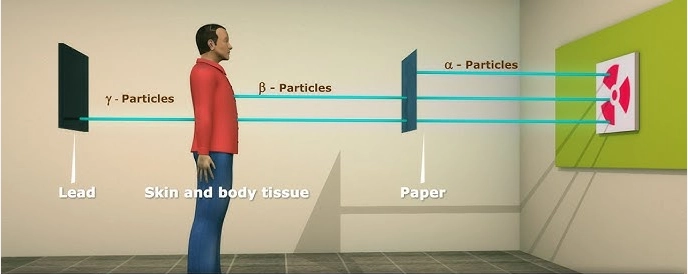Alpha particlesi. They are slightly deflected by the electric field towards the negative plate. This means that the alpha particles are heavy positively charged particles.ii. They are slightly deflected by magnetic fields towards the South Pole. iii. They have high ionisation power i.e. they can easily knock out electrons from an atom. iv. They have low penetrating power. In air they travel a few centimetres before they are stopped. In addition, a thin sheet of paper easily absorbs alpha particles. v. These properties suggest that alpha particles are helium nuclei 42𝑯𝒆. Beta particlesi. Beta particles are strongly deflected toward the positive plate in the electric field. They are, therefore, light particles carrying a negative charge.ii. Magnetic field deflects beta particles towards the south poles. iii. They have low ionising power. iv. Beta particles have high penetrating power. They can travel a few metres in air before they are absorbed. Beta particles penetrate materials, whereas alpha particles cannot. Beta particles are absorbed by an aluminium sheet a few millimetres thick. v. Beta particles have been confirmed to be high energy (very fast moving electrons (01𝑒) Gamma Raysi. Gamma rays are not deflected by electric and magnetic fields. They are therefore not charged particles.ii. They have little or no ionisation ability. iii. They have the highest penetrating power and can penetrate most materials. Dense materials like lead absorbs gamma radiation. iv. Gamma rays are high-energy electromagnetic waves with very high frequency and very short wavelength. |
The students listen and observe the activities. | properties of radioactive radiations | |
| STEP 4: APPLICATION Entire class |
The teacher ask the students to read through all they have copied and give more discussion/explanation as directed by the teacher. They take corrections where they are wrong. | The students did what the teacher ask them to do. | Better understanding of models of the atom. |
| STEP 5: EVALUATION Individual students |
The teacher asks the students questions to test them. 1. What is radioactivity? 2. What are the advantages and disadvantages of radioactive substances? 3. A radioactive nuclide has a high decay rate. What does this mean for its half-life and activity? 4. Calculate the age of the Shroud of Turin given that the amount of 14C found in it is 92% of that in living tissue. [half-life of 14C is 5730 y] |
Students expected answers 1. Radioactivity is the spontaneous decay or disintegration of the nucleus of the atom of an element during which it emits α, β or γ rays or a combination of any or all the three and energy ( or heat). ADVANTAGES OF RADIOACTIVE SUBSTANCES a). They are used in medical practice in treating malignant growth in the same way the x-ray is used. b). They form main source of nuclear fuel used in generating nuclear energy. c). Radioactive isotopes are used in tracer technique. d). They are used in estimating age of archaeological findings. DISADVANTAGES OF RADIOACTIVE SUBSTANCE a). Emitted radiation destroys tissue cell exposed to it. b). It upsets chemical reaction taking place in blood cells which undoubtedly lead to death. 3. Half-life is inversely related to decay rate, so the half-life is short. Activity depends on both the number of decaying particles and the decay rate, so the activity can be great or small. 4. Knowing that 92% of the 14C remains means that N/No = 0.92 N/No = e−λt 0.92 = e−λt ln0.92 = −λt −0.0834 = −λt t = 0.0834/λ But λ = 0.693/t1/2 λ = 0.693/5730y λ = 1.2 × 10-4 :. t = 0.0834/λ t = 0.0834/1.2 × 10-4 t = 689.58y ≈ 690y This dates the material in the shroud to 1988–690 = a.d. 1300. Our calculation is only accurate to two digits, so that the year is rounded to 1300. The values obtained at the three independent laboratories gave a weighted average date of a.d. 1320±60. The uncertainty is typical of carbon-14 dating and is due to the small amount of 14C in living tissues, the amount of material available, and experimental uncertainties (reduced by having three independent measurements). It is meaningful that the date of the shroud is consistent with the first record of its existence and inconsistent with the period in which Jesus lived. |
Asking the learners questions to assess the achievement of the set objectives. |
|
| |||
| CONCLUSION | The teacher concluded the lesson Radioactivity is a spontaneous process, it involves the spontaneous emission of particles and radiation from the nucleus of unstable atoms. Isotopes, radioactive elements, and the concepts of half-life and decay constant are crucial in understanding and quantifying radioactive decay processes. Radioactivity goes on independent of external control, it is not affected by temperature, or pressure or by chemical treatment. It is a random process as no one can predict which atom will disintegrate at a given time. |
The students write down the conclusion of the lesson and listen attentively. | Better understanding of Radioactivity. |
| ASSIGNMENT | The teacher gives learners take home. 1. If the half life of a radioactive substance is 2.45 × 108s, determine is decay constant. 2. The phenomemon of radioactivity was first discovered by (A) Marie Curie (B) J.J. Thompson (C) Henri Becquerel (D) Nent Bohr (E) Enrico Fermi 3. A radioactive substance has a half-life of 3 days. If a mass of 1.55g of this substance is left after decaying for 15 days, dertermine the original value of the mass (A) 49.6g (B) 37.2g (C) 24.8g (D) 12.4g 4. Which of the following is usually used to cause fission in an atomic reactor? (A) alpha particles (B) beta particles (C ) electrons (D) neutrons 5. A substance has a half-life 30 mins after 6mins the count rate was observed to be 400. What was its count rate at zero time. (A) 200 (B) 1200 (C) 1600 (D) 2400 6. A nuclide 20284Y emits in succession an α-particle and β-particle. The atomic number of the resulting nuclide is (A) 198 (B) 83 (C ) 82 (D) 80. 7. (a) Define radioactivity; half-life and decay constant. (b) Write down the relation between half-life and decay constant (c) In 180 minutes, the activity of a certain radioactive substance falls to one–eight of its original value. Calculate its half-life. 8 (a) A nuclide × emits β-particle to form a daughter nuclide Y. write a nuclear equation to illustrate the charge conservation. (b) the isotope of a nuclide has a half-life of 5.4 × 103s. Calculate its decay constant. 9. Define the following terms (a) Conduction (b) Convection (c) Radiation 10. With the aid of a diagram, explain how the construction of a thermos flask minimizes heat exchange with the surrounding. 11. If a nucleus 31H decays, a nucleus of 32H is formed accompanied with the emission of (a) beta particles (b) gamma particle (c) alpha particle (d) x-rays. 12. The count rate of radioactive substances diminishes from 600 to 150 in 60 secs. Determine the half life of the substance (a) 15 secs (b) 30 secs (c) 45 secs (d) 60 secs. 13. A radioactive substance half life of 20 hrs. What fraction of the original radioactive nuclide will remain after 80 hrs (a) 1/32 (b) 1/16 (c ) 1/8 (d) 15/16 14. A material of mass 1.0 × 10-3kg undergoes fission process which decreases its mass by 0.02%. Calculate the amount energy released in the process [c = 3 × 108m/s] (A) 1.8 × 1020J (B) 1.8 × 10 15. In a nuclear reaction the mass defect is 2.0 × 10-6g. Calculate the energy released, given velocity of light is 3 × 108m/s. (A) 9.0 × 1007J (B) 1.8 × 1008J (C) 1.8 × 1009J (D) 9.0 × 10-10J 16. Explain the terms nuclear fission and nuclear fusion 17. Nuclear reaction is given by the equation 21H + 31H → 42H + 10n + energy (a) What type of nuclear reaction is it? (b) state two component in a nuclear reactor used to control chain reaction |
The learners copy the assignment | Better understanding of Radioactivity. |
