Light waves
Refraction of Light
Subject: Physics
Theme: Waves-Motion Without Material Transfer
Topic: Light waves
Sub Topic: Refraction of Light waves
Date: dd/mm/yyyy
Class: S.S.S 2
Duration: 40 Minutes
No of Learners: 40
Learning Objectives: By the end of the lesson learners should be able to:
1. Explain Refraction of light
Refraction is the bending away of light from the normal as it passes from one medium to the other.There is a change in the direction and speed of a ray of light when it passes from medium to another medium of different density. This change in the direction of the light of the light ray which is due to difference in the speed of light in different media is called refraction.
When a ray of light travels from optically less dense medium (air) to an optically dense medium (water, glass), it bends towards the normal.
A ray passing from glass or water to air is bent away from the normal.
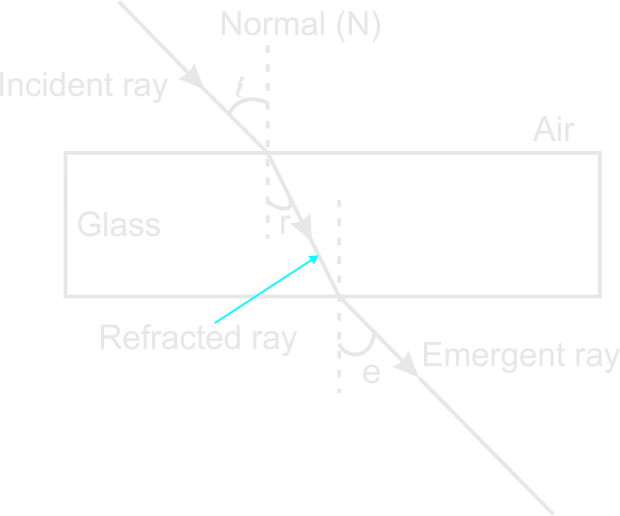Refraction of light ray
2. state the laws of refraction
1. The incident ray, refracted ray and the normal at the point of incidence; all lie on the same plane.2. The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant for a given pair of media.
The second law is known as Snellβs law.
π = sin π / sin π
The constant, n, is known as the refractive index of the second medium with respect to the first medium. It is a number which gives a measure of refraction or bending of light as it travels from one medium to another. As the ray of light travels from air to glass, the refractive index can be written as:
πππ = sin π / sin π
From the principle of reversibility of light
πππ = 1/πππ
Furthermore,
πππ = πππππ ππ πππππ ππ πππ (πππ πππ π, πππππ ππππ πππ πππ) / πππππ ππ πππππ ππ πππππ (πππ πππ π, ππππππππππ πππ πππ)
3. Explain the Effects of refraction
The phenomenon of refraction is responsible for the following:1 The bottom of a clear river or pond appears shallower than it really is.
2 A rod or spoon appears bent or broken when it is partially immersed in water or any liquid.
3 Letters in print seem to be nearer when we place a thick block of glass over them.
4. Determine the Refractive index of a rectangular/triangular glass block prisms
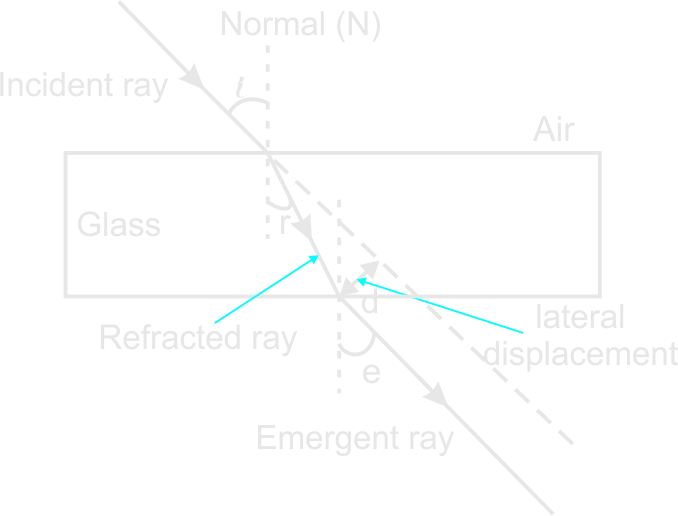Rectangular glass block prisms
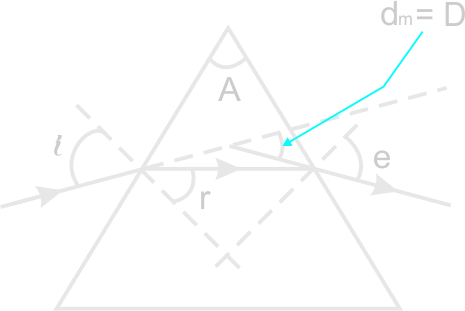Triangular glass block prism
Angle of deviation is the smallest angle at which light is bent by an optical system or element. Or is the angle between the incident ray produced and the emergent ray produced. It decreases with an increase in the angle of incidence.
Totally reflecting prism is a prism with two refracting surfaces that meet at a 90 degree angle and two other angles that are each 45 degrees or a prism having one of the angles as between two refracting surfaces and the other two angles.
The prism deviates the incident ray through an angle known as angle of deviation. This is the angle between the incident ray and the emergent ray of light passing through a prism. The amount of deviation is determined by:
(a) the angle of incidence,
(b) the refracting angle (A) of the prism and,
(c) the refractive index of the material of the prism. Experiments show that the angle of deviation (d) varies with the angle of incidence (i)
At minimum deviation, i = e
There is thus a minimum angle of deviation (D) and this occurs when the incident and emergent rays are equally inclined to their respective surfaces. The ray passes symmetrically through the prism and the angle of incidence equals angle of emergence (i = e)
It can be shown that at minimum deviation (D), the refractive index (n) of the glass, the refractive angle (A) of the prism and the angle of minimum deviation (D) are related by the equation.
Thus by measuring the angle of minimum deviation and the refracting angle of the prism, we can calculate the refractive index of the material of the prism.
The refractive index, n = sin 1/2(A + D)/sin A/2
Total Internal Reflection in Rectangular Prism
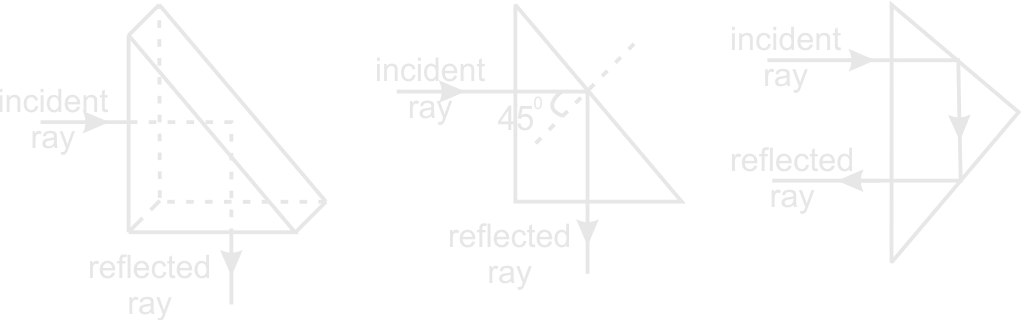Total Internal Reflection in Triangular Prism
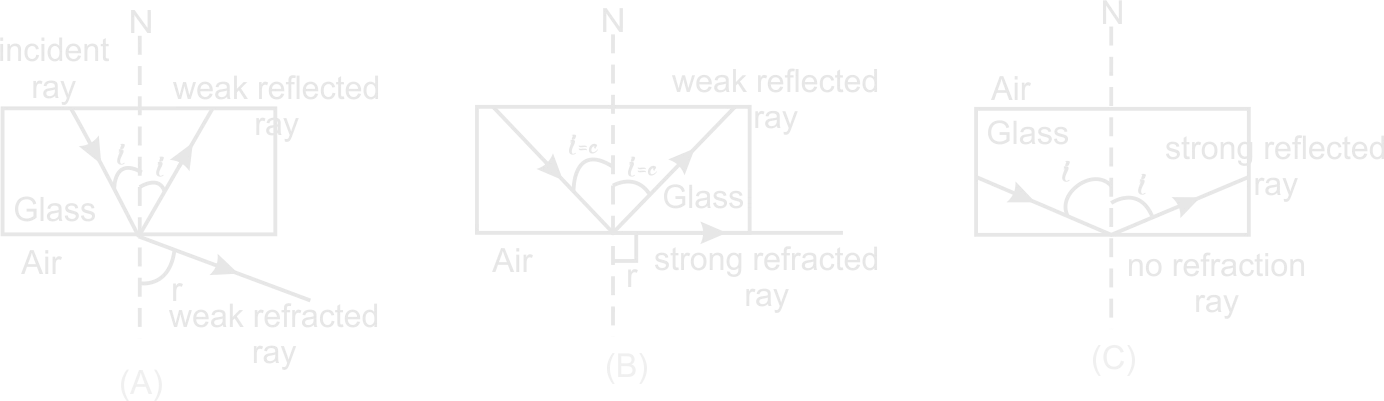
When light passes at a small angle of incidence from a denser to a less dense medium e.g. from glass to air, there is a strong refracted ray. There is also a weak ray reflected back into the denser medium.
When the angle of incidence increases, the angle of refraction also increases.
At a certain increase of the angle of incidence, the angle of refraction is 900. This angle of incidence in the denser medium for which the angle of refraction in the less dense medium is 900, is referred to as the critical angle (c).
For angle of incidence greater than C, the refracted ray disappears and all the incident light is reflected back into the denser medium. At this point, the ray is said to experience total internal reflection.
Example of total internal reflection is the mirage on the road, where the refractive density of warm air is less than that of cool air and light meets a layer at a critical angle, it suffers total internal reflection.
Hence,
Critical Angle
The critical angle is the angle of incidence in denser medium when the angle of refraction in less dense medium is 900Total Internal Reflection
The total internal reflection is the reflection of an incidence ra of light at the interface between the medium of incidence and another medium of lower refractive index when the angle of incidence in the denser medium exceeds the critical angle.Applications of total internal reflection
1. It is used in optical fibres.2. It is applied in telecommunications
3. It occurs in a mirage in a desert or on a hot summer day
Diadvantages of total internal reflection
The disadvantage of total internal reflection is production of evanescent waves which are beyond the surface of the boundary. This is caused due to the fact that some of the light gets penetrated into the second medium on the point of their boundary.Relationship between Critical Angle and Refractive index
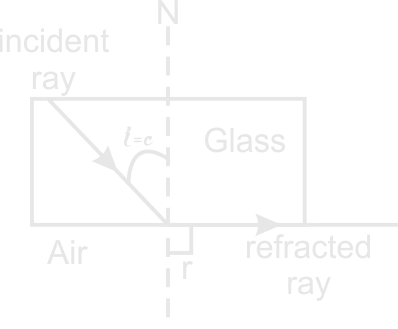Critical Angle and refractive index
From Snell's laws
ang = sin i / sin r
:. gna = sin c / sin 900 gna = sin c / 1
sin c = gna
But n = ang = 1/gna
:. sin c = 1/n
NOTE: Refractive index (n) of glass is 1.5
sin c = 1/1.5
sin c = 0.6667
c = sin-1 0.6667
c β 420
Hence, for any angle of incidence in glass greater than 420, there is total interanal reflection. Example 1.
A ray of light experience a minimum deviation when passing symmetrically through an equilateral triangular glass prism. Calculate the angle of incidence of the ray. (Refractive index of glass = 1.5)
Solution
the Refractive angle (A) of an equilateral triangular prism is 60 degrees,
at minimum deviation, angle of refraction r = A/2
r = 600/2
r = 30Β°
Refractive index (n) = 1.5
n = sin i/ sin r
1.5 = sin i / sin 300
sin i = 1.5 Γ 0.5
sin i = 0.75
i = sin-i 0.75
i = 48.6Β°.
Example 2.
What is the critical angle for light travelling from water to air? Refractive index of water = 4/3
Solution
n = 1/sin c
4/3 = 1/sin c
0.74 = 1/sin c
c = sin -1 0.74
c = 48036'
Example 3.
The angle of incidence f a ray of light striking an equilateral triangular prisms ABC of refracting angle 600 is400. Calculate;
(i) the angle of refraction at the first face
(ii) the angle of emergence
(iii) if the light is incident normally on the first face AB, describe with the aid of a diagram what is the fate of this light as it passes through the prisms.
Solution
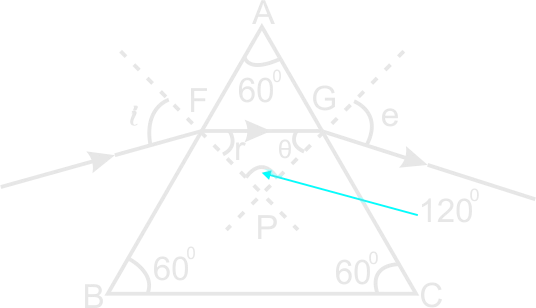
(i) let r = refraction at first face AB
From Snell's law
n = sin i / sin r
i.5 = sin 400 / sin r
sin r = sin 400 / 1.5
sin r = 0.6428/1.5
sin r = 0.4285
r = sin-1 0.4285
r = 25.370
r = 250 22'
(ii) Let the angle of emergence be e
Consider the figure AFPG
angle AFP + angle AGP = 1800
Also, angle FAG + angle GPF = 1800
But angle FAG = 600
:. angle GPF = 1800 - 600
angle GPF = 1200
:. r + ΞΈ + 1200
r + ΞΈ = 1800 - 1200
r + ΞΈ = 600
But r = 25.370
25.370 + ΞΈ = 600
ΞΈ = 600 - 25.370
ΞΈ = 34.630
ΞΈ0 is the angle of incidence on the glass-air boundary on the face AC
:. n = sin i / sin r
1/n = sin r / sin i = gna
1/n = sin ΞΈ / sin e
1/1.5 = sin 34.63 / sin e
sin e = 1.5 x sin 34.630
sin e = 0.8524
e = sin-1 0.8524
e = 58.470
e = 580 30'
(iii)
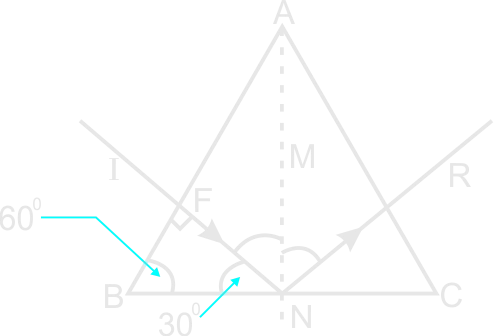
The incident ray "IF" is normal to the face AB. It therefore passes through undeviated and strikes the face BC at N.
:. angle FNM = 600
But sin c = 1/n = 1/1.5
But, critical angle of glass β 420
:. Since 600 > 420
theangle of incidence is greater than the critical angle.
The ray IN is hence taotally internally reflected at N as shown in the figure above.
Hence, there is no emergent ray.
4. Explain REAL AND APPARENT DEPTH
A thick slab of glass appears to be only two βthird of its real thickness when viewed vertically from above. Similarly, water in a pond appears to be only three quarters of its real depth. Rays from a coin at the bottom of a bucket of water are refracted away when they leave water and enter the eyes. They appear as if coming from a virtual image, which is apparent depth while the actual depth of the bottom remains and is referred to as real depthRefractive index (n) = real depth (D) / apparent depth (d)
Example 1.
If the real depth of a river bed is 10m and the apparent depth is 7.5m. Find the refractive index of the river water?
Solution
n = real depth/apparent depth
n = 10/7.5
n = 1.33
Therefore the refractive index is 1.33
Example 2.
What is the real depth of a swimming pool which appears to be 10m deep whan viwed directly from above its surface? (Refractive index of water = 4/3).
Solution
n = real depth/apparent depth
4/3 = real depth/10
real depth = 40/3
real depth = 13.13m
Rationale:
A thick slab of glass appears to be only twoβthird of its real thickness when viewed vertically from above. Similarly, water in a pond appears to be only three quarters of its real depth. Rays from a coin at the bottom of a bucket of water are refracted away when they leave water and enter the eyes. They appear as if coming from a virtual image, which is apparent depth while the actual depth of the bottom remains and is referred to as real depth.Prerequisite/ Previous knowledge:
Production and propagation of wave.Learning Materials:
A cardboard containing diagram of total internal reflection etc.Reference Materials:
1. New School Physic for Senior Secondary Schools, by M. W. Anyakowa.2. Lamlas's SSCE and UTME, by O. Ajaja and H. B. Olaniyi.
3. Okeke P.N and etal (2011), Macminian, Senior Secondary School Physics, New Edition.
4. Farinde E.O and etal (2015), Essential Physics. 6th Edition,
Lesson Development:
STAGE |
TEACHER'S ACTIVITY |
LEARNER'S ACTIVITY |
LEARNING POINTS |
|---|---|---|---|
| STEP I: PREVIOUS KNOWLEDGE full class session |
The teacher asks learners questions based on previous knowledge. 1. What is light? 2. Name one matter that travels faster than light. 3. What is the speed of light? 4. What is rectilinear propagation of light? 5. What type of wave does light falls into? 6. What is reflection? 7. State the laws of relection. 8. List and explain Objects light falls on. 9. Differentiate between Ray of light and Beam of light. 10. List and explain types of beam. |
Learners' response to teacher's question. 1. Light is a visible form of energy that radiates from its source. 2. There is nothing that travels faster than light. 3. Light travels very fast at a speed of 300000000 m/s (3x108 m/s). 4. Light travels on a straight line. The phenomenon is called rectilinear propagation of light. 5. Light does not require material medium for it propagation or transmission, hence Light is an electromagnetic wave (because it does not require material medium). 6. Reflection of light is the sending back of light ray which fall at the surface of an object. 7. Law of reflection states that: The incident ray, the reflected ray and the normal at the point of incidence all lie in the same plane. 8. Objects light falls on are: (a) Transparent objects: are substances which allow light energy to pass through it e.g glass, beaker e.t.c. (b) Translucent object: a substance which allow light to pass through it but is not clearly seen e.g oiled paper, plastic bags e.t.c. (c) Opaque objects: are objects which do not allow light to pass through them e.g wood, human being. 9. Ray of light: It is the pathway through which light travels in a straight line while beam of light is the collection of rays of light is called beam of light.There are three types of beam of light. 10. (a) Parallel beam: Is the collection of rays moving in a straight line parallel to each other. (b) Convergent beam: Is the collection of light which meet at a point. (c) Divergent beam: Is the collection of light rays which go out from a point. |
Confirming previous knowledge. |
| STEP II: INTRODUCTION full class session |
The teacher introduce the topic for discussion. Refraction of light Refraction of light is the bending of light, as it passes from a less dense medium to a denser medium. The light ray may bend towards the normal. Laws of refraction states that: 1. The incident ray, the refracted ray and normal to the point of incidence all lie in the same plane. 2. The second law states that: the ratio of the sine of the angle refraction is constant for any ray passing from one medium to another. The second law is known as snellβs law. The law was named after scientist Willer Brod Snellius who formulated it. When light rays travels from a less dense medium (air) to a denser medium (water), the refracted rays is bent towards the normal. When light rays leaves from denser medium (water) to a less dense medium (air), the refracted ray is bent away from the normal. |
Learners listen to teacher, ask questions and make contribution. | Developing the idea of the topic, refraction of light. |
| STEP III: EXPLORATION What is Refraction? |
The teacher asks the learners probing question. Why does light undergo refraction as it travells from one medium to another? | Learners' expected answer Refraction is the bending away of light from the normal as it passes from one medium to the other. There is a change in the direction and speed of a ray of light when it passes from medium to another medium of different density. This change in the direction of the light of the light ray which is due to difference in the speed of light in different media is called refraction. When a ray of light travels from optically less dense medium (air) to an optically dense medium (water, glass), it bends towards the normal. A ray passing from glass or water to air is bent away from the normal |
Definition of refraction. |
| STEP IV: DISCUSSION Laws of Refraction |
The teacher asks learners to state the laws of refraction, and guides learners to explain Snell's law. | Learners espected answer. LAWS OF REFRACTION 1. The incident ray, refracted ray and the normal at the point of incidence; all lie on the same plane. 2. The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant for a given pair of media. The second law is known as Snellβs law n = sin i /sin r The constant, n, is known as the refractive index of the second medium with respect to the first medium. It is a number which gives a measure of refraction or bending of light as it travels from one medium to another. As the ray of light travels from air to glass, the refractive index can be written as: ang = sin i /sin r From the principle of reversibility of light ang = 1/gna Furthermore, ang = speed of light in air (medium 1, incidence medium)/speed of light in glass (medium 2, refractive medium) |
Laws of Refraction |
| STEP V: APPLICATION Total Internal refraction and critical angle |
The teacher guides the students as follows. TOTAL INTERNAL REFLECTION AND CRITICAL ANGLE When a light ray passes from a medium, say air to glass, most of the light is refracted, but a small percentage is reflected THE CRITICAL ANGLE: The critical angle is the incident angle at which the angle of reflection is 90Β° when light passes from denser to less dense medium. CONDITIONS NECESSARY FOR TOTAL INTERNAL REFLECTION TO OCCUR 1. Light must be traveling from a dense to a less medium 2. The angle of incidence in the denser medium must be greater than the critical angle REAL AND APPARENT DEPTH A thick slab of glass appears to be only two βthird of its real thickness when viewed vertically from above. Similarly, water in a pond appears to be only three quarters of its real depth. Rays from a coin at the bottom of a bucket of water are refracted away when they leave water and enter the eyes. They appear as if coming from a virtual image, which is apparent depth while the actual depth of the bottom remains and is referred to as real depth Refractive index = real depth/apparent depth |
The students listen, contribute and ask question | Total Internal refraction and critical angle |
| STEP VI: EVALUATION | The teacher asks the learners questions. 1. What is the critical angle for light travelling from water to air? Refractive index of water = 4/3 2. What is the real depth of a swimming pool which appears to be 10m deep whan viwed directly from above its surface? (Refractive index of water = 4/3). |
The learners answer the teacher's questions. 1. Solution n = 1/sin c 4/3 = 1/sin c 0.74 = 1/sin c c = sin -1 0.74 c = 48036' 2. Solution n = real depth/apparent depth 4/3 = real depth/10 real depth = 40/3 real depth = 13.13m |
Ask the learners questions to assess the achievement of the set objectives. |
| CONCLUSION | The teacher concluded the lesson with the students. The following are effects of refraction: 1) Apparent depth of a swimming pool. 2) Apparent bending of a stick partly immersed in water. 3) Briging objects into view. E.t.c. |
The students listen and make contribute | Effects of refraction. |
| ASSIGNMENT | The teacher gives learners a take home. | 1. A ray of light is incident on an equilateral triangular glass prism of Refractive index 3/2. Calculate the angle through which the ray is minimally deviated in the prism? 2. The velocities of light in air and glass are 3.0 x108 m/s and 1.8 x108 m/s respectively. Calculate the sine of the angle of incidence that will produce an angle of refraction of 300 for a ray of light incident on glass. 3. What is the real depth of a swimming pool which appears to be 12m deep when viewed directly from above its surface? ( refractive index of water = 4/3)? 4. what is the critical angle for light travelling from water to air. Refractive index of water = 4/3? 5. State the laws of refraction. |
Improving their level of understanding on Refraction of Light ray. |