Teaching Method in Futher Mathematics
Asei Lesson Plan on Further Maths - Matrices
Theme: Matrices
Topic: Matrices
Sub Topic: Basic Concepts of Matrices
Date: dd/mm/yyyy
Class: SSS 3
Duration: 35 Minutes
No of Learners: 30
Learning Objectives:
By the end of the lesson learners should be able to:Defined Matrices
A Matrix is a rectangular array of numbers or elements that are enclosed within brackets. E.g.
Describe the elements, row, column and order of matrices.
E.g.
Identify and describe the notation of a matrix. e.g
Solve questions on Equality of Matrices.
Two matrices are said to be equal if corresponding elements throughout are equal. The two matrices must also be of the same order. E.g.
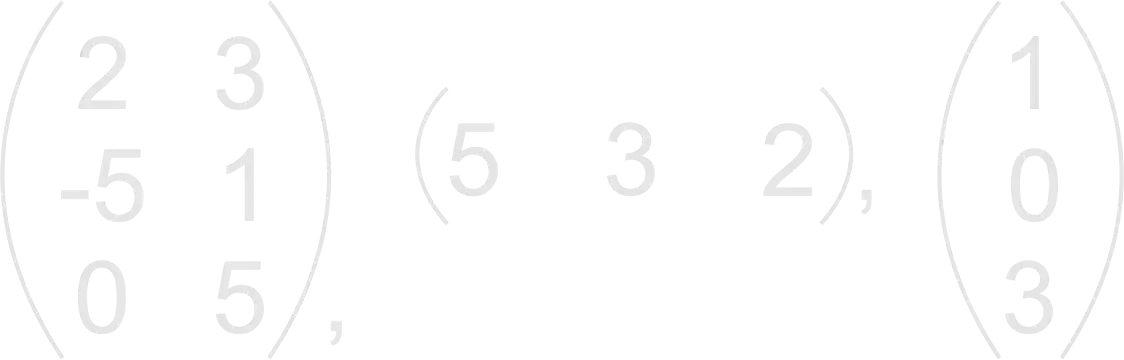
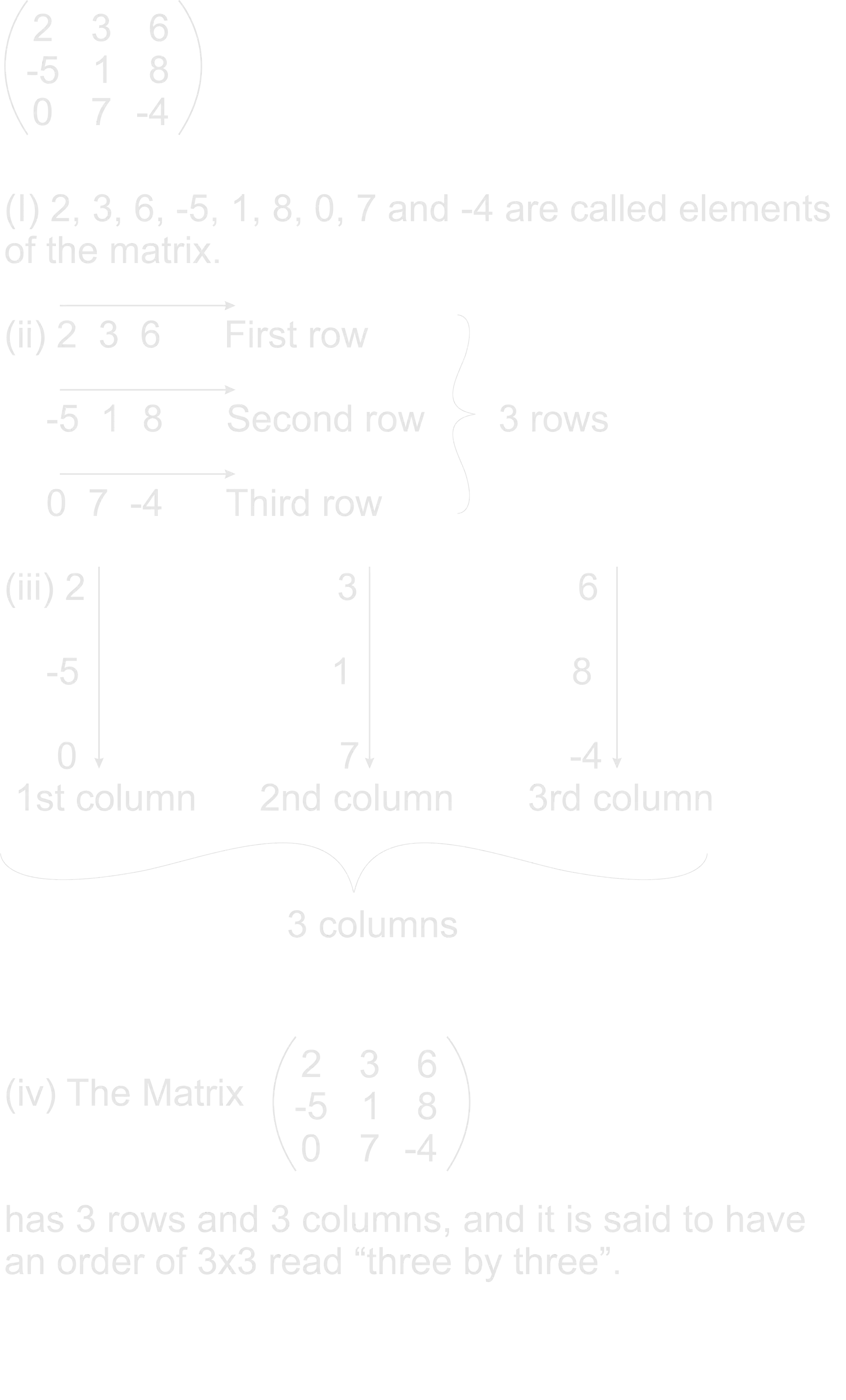
NOTE: In describing the matrix, the number of rows is started first and the number of columns second. In general, a matrix with m-rows and n-columns is said to have an order of mxn.
A matrix with only one row of elements is called a row or line matrix. E.g. ( 4 8 -2 0 5 ), while a matrix with only one column of elements is called a column matrix.

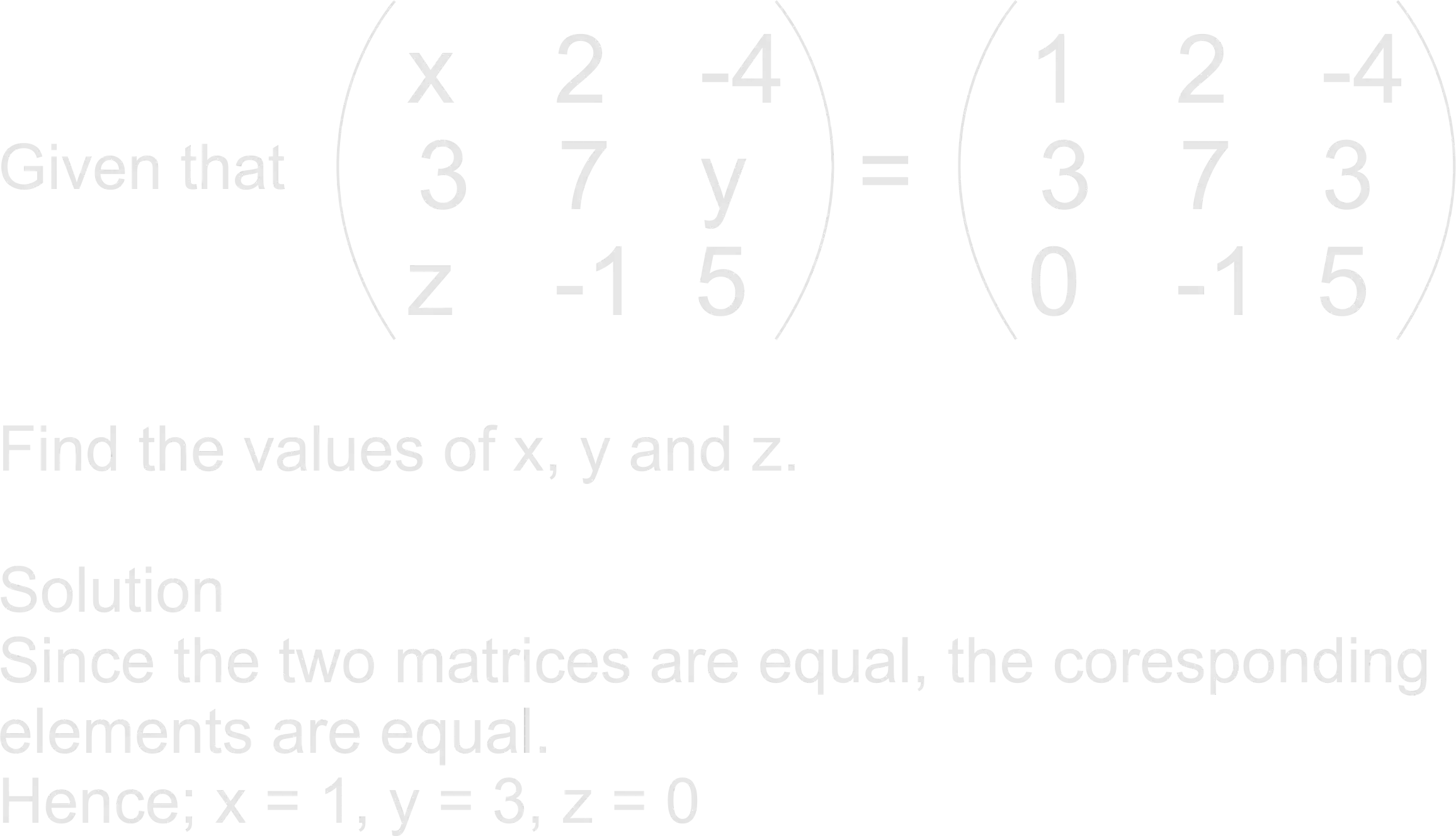
Rationale:
In computer-based applications, matrices play a vital role in the projection of three-dimensional images into a two-dimensional screen, creating realistic seeming motions. Digital Images have spaced collections of pixels or image elements arranged in 2d space and in computers they are represented as Matrices. These matrices contain different values of integers which represent the level of brightness or intensity or similar properties. It is therefore important for students to be taught Matrices.
Prerequisite/ Previous knowledge:
Learners have learnt the Binary format for communication by the computer.
Learning Materials:
Pictures of encryption of message codes, binary format for communication, colour pixel used by the computer.
Reference Materials:
- Further Mathematics Project 3 by Tuttuh-Adegun, M.R. Sivasubramaniam, S. Adegoke, R
- Engineering Mathematics by K. A. Stroud
Lesson Development:
| STAGE | TEACHER'S ACTIVITY | LEARNER'S ACTIVITY | LEARNING POINTS |
|---|---|---|---|
| INTRODUCTION full class session (5mins) |
The teacher asks learners to identify the following picture on the board.
Through question and answer teacher guides the learners to solve the following binary matrix format for communication by the computer to Decimal Equivalent in Human understanding.
|
Learners expected to respond; The diagram on the board is a Binary Matrix.
|
Learner’s entry points. NOTE: |
| DEVELOPMENT Step 1. Group Work (2 mins) | The teacher guides the learners to form four groups and ask them to choose their leaders and secretaries. | Learners choose their group leaders and secretaries. | Inculcating leadership skills, competitive spirit, cooperation, teamwork and a sense of responsibility among learners. |
| Step 2 Full class session (7mins) | The teacher should explain the importance & application of matrices as used by the computer to process data and give out information e.g in graphics presentation, communication etc, this will enable learners to develop interest & appreciate the concepts of the topic. Guide learners in activities that lead them to the definition of a matrix, element of matrix, row, column and order of the matrix. The teacher gives the four groups a printout of RGB (Red Green Blue) colour code. 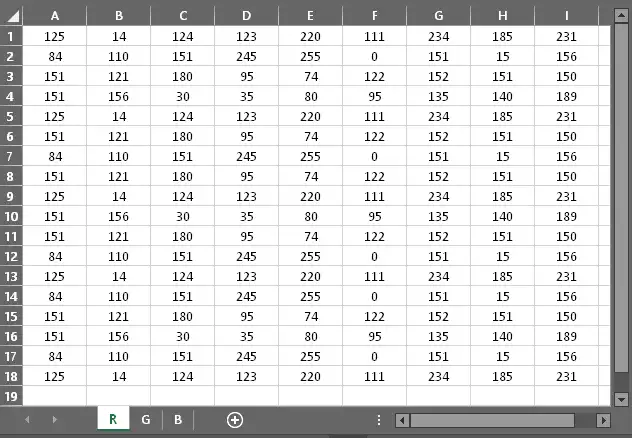

and ask them to explain or describe the figure placed before them. Teacher to encourage vibrant brainstorm of ideas and facilitate students’ participation and clarify or render help if necessary in the activity. |
Learners expected response;
|
Developing the definition of a matrix from the activity. |
| The teacher then tell learners that the figure with the brackets are matrices and ask learners to define matrix in their own words. | Learners expected to respond.
|
Definition of Matrix. | |
| The teacher then asks learners to identify the elements, numbers of rows, numbers of columns and order in each matrix in the figures above. The teacher should inform learners that in describing the matrix, the number of rows is started first and the number of columns second. In general, a matrix with m-rows and n-columns is said to have an order of mxn. |
Learners expected to respond.
|
Identifying the elements, rows, columns and order of matrices. | |
| Stage 3 Full class discussion (10 mins) |
The teacher guides learners to identify the notation of each element in the matrix below.
The teacher explains to learners that the matrix. 
is denoted by bold faces capital letters, while the elements of the matrix are denoted by small letters with a suffix that uniquely defined the exact positions of each element in the array. |
Learners follow the teacher's procedures to identify and list the notation of each element in the matrix.
|
Identifying and describing the notation of an element of a matrix. |
The teacher guides learners to solve the following question.
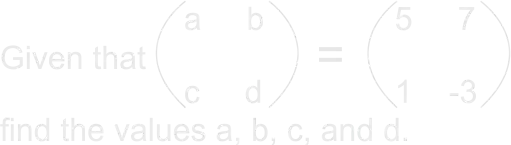
The teacher explains to learners that two matrices are said to be equal if corresponding elements throughout are equal. hence, the two matrices must also be of the same order. |
learners expected to respond; SolutionSince the two matrices are equal, their corresponding elements are equal.
|
Equality of matrices. | |
| Evaluation. Full class session (10 mins) | Ask the following questions to evaluate the achievement of the set objectives.
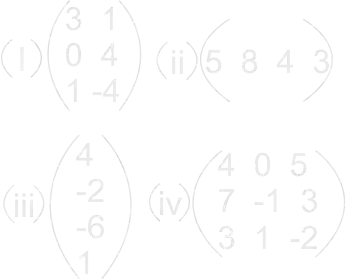
Find; |
Learners expected response:
|
Confirming the achievement of the set objectives. |
| Conclusion, full class session (3 mins) | Ask learners, 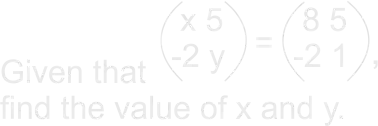
|
Learners expected response. Matrices that have the same order are said to be equal if their corresponding elements are equal. |
Acquiring/ improving understanding of the Basic Concepts Matrices. |
| ASSIGNMENT | The teacher gives learners a take home.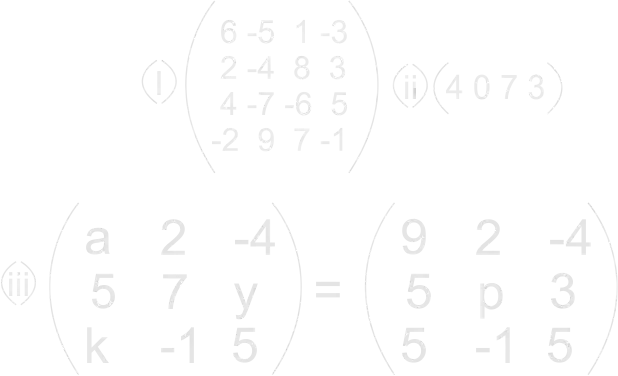
|
Learners answer other questions. | Improving their level of understanding of Matrices. |